Teymur Valiyev Weblog

Data Structure

28 March 2018 · Filed in Tutorial

Abstract Data Type

An Abstract Data Type (ADT) is the specification of a group of operations that make sense for a given data type.

Primitive data types

Primitive data types are those with built-in support in the programming language you’re using—they work without external modules. These always include integers, floating points, 3 and generic operations with them (addition, subtraction, division).

Structures

An Abstract Data Type only describes how variables of a given data type are operated. It provides a list of operations, but doesn’t explain how data operations happen. Conversely, data structures describe how data is to be organized and accessed in the computer’s memory. They provide ways for implementing ADTs in data-handling modules.

Abstract Data Types

Abstract Data Type Other Common Names Commonly Implemented With
List Sequence Array,Linked List
Queue   Array,Linked List
Double Ended Queue Equeue, Deque Array,Doubly Linked List
Stack   Array,Linked List
Associative Array Dictionary, Hash Map, Hash, Map Hash Table
Set   Red-Black Tree,Hash Table
Priority Queue Heap Heap

Container List Set Multiset Map Multimap Graph Stack Queue Priority queue Double-ended queue Double-ended priority queue

Linear Data Structures

Hash-Based Data Structures

Trees

Binary Search Trees

Heaps

Graphs

Strings

Lists

A list is an abstract data type used for storing sequential items

The head is the first item in the list.
The tail is all remaining items. 
The tail is itself a list, having its own head and tail:
Function Functionality
new Creates an empty list.
append Adds an item to the end of the list.
prepend Adds an item to the beginning of the list.
head Returns the item at the beginning of the list.
tail Returns all items except the head. If the list only has 1 item, returns an empty list.
is_empty Returns a bool indicating whether or not the list contains any items.

Stack

Stack can be implemented with a variety of data structures, such as a linked list or an array

LIFO data structure. LIFO stands for Last-in-first-out.

Function Functionality
push(i) Insert element i at the top of the stack.
pop() Remove the element at the top of the stack.
peek() returns the element at the top of the stack without changing the stack
size() returns the current size of the stack
isFull() check if stack is full.
isEmpty() check if stack is empty.

Time Complexity

Function Linked list Array
push() O(1) O(1)
pop() O(1) O(1)

Queue

Queue is an abstract data structure, somewhat similar to Stacks. Unlike stacks, a queue is open at both its ends. One end is always used to insert data (enqueue) and the other is used to remove data (dequeue). Queue follows First-In-First-Out methodology, i.e., the data item stored first will be accessed first.

Function Functionality
enqueue(i) Insert element i at the tail of the queue.
dequeue() Remove the element at the head of the queue.
peek() returns the element at the head of the queue without changing the queue.
size() returns the current size of the queue
isfull() Checks if the queue is full.
isempty() Checks if the queue is empty.

Time Complexity

Function Linked list Array
enqueue() O(1) O(n)
dequeue() O(1) O(n)

Double Ended Queues

Double ended queues, called deques for short, are a generalized form of the queue. It is exactly like a queue except that elements can be added to or removed from the head or the tail

Function Functionality
append(i) Adds element i to the tail of the queue
prepend(i) Adds element i to the head of the queue
delete_last() Removes the element at the tail of the queue
delete_first() Removes the element at the head of the queue
examine_last() Returns the element at the tail of the queue
examine_first() Returns the element at the head of the queue

Time Complexity

Operation Doubly Linked List Dynamic Array
append O(1) O(1)
prepend O(1) O(n)
delete_last O(1) O(1)
delete_first O(1) O(n)
examine_last O(1) O(1)
examine_first O(1) O(1)

Priority Queue

Priority queues are a kind of abstract data type that generalizes the queue. Their principles are exactly the same except that they also include a priority for every value in the queue. When a value is inserted, a priority is assigned to it. The value with the highest priority is always removed first.

Function Functionality
insert(i, p) Add value i with priority p.
pop() Remove and return the element with the highest priority.
peek() Return the element with the highest priority without changing the queue.

Time Complexity

Function Heap
insert(i, p) O(logn)
pop() O(logn)
peek() O(1)

Sets

Sets are a type of abstract data type that allows you to store a list of non-repated values. Their name derives from the mathematical concept of finite sets. Unlike an array, sets are unordered and unindexed These are the two properties of a set: the data is unordered and it is not duplicated.

Function Functionality
insert(i) Adds i to the set
remove(i) Removes i from the set
size() Returns the size of the set
contains(i) Returns whether or not the set contains i
union(S, T) Returns the union of set S and set T
intersection(S, T) Returns the intersection of set S and set T
difference(S, T) Returns the difference of set S and set T
subset(S, T) Returns whether or not set S is a subset of set T

Time Complexity

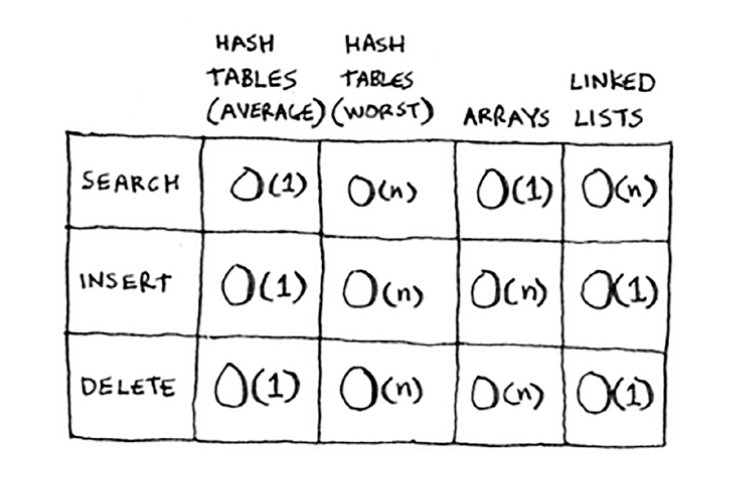
A hash table is the most common data structure

Function Hash table
insert() O(1)
contains() O(1)
remove() O(1)

Array

The array is a basic abstract data type that holds an ordered collection of items accessible by an integer index. These items can be anything from primitive types such as integers to more complex types like instances of classes. Since it’s an ADT, it doesn’t specify an implementation, but is almost always implemented by an array (data structure) or dynamic array. They are extremely ubiquitous and among the oldest, most widely used data structures in programming.

Unless otherwise specified, for the remainder of this wiki, the word “array” will refer to the data structure and not the abstract data type.

Arrays are often used to implement abstract data types such as arrays (ADT) and stacks.

In Java, you can create an array of any primitive data type, abstract data type, or custom class. Java also provides an ArrayList type which gives you more flexibility.

Following are the basic operations supported by an array.

  • Traverse − print all the array elements one by one.
  • Insertion − Adds an element at the given index.
  • Deletion − Deletes an element at the given index.
  • Search − Searches an element using the given index or by the value.
  • Update − Updates an element at the given index.
Operation Array ArrayList Linked List
Read O(1) O(1) O(n)
Add/Remove at end O(1) O(1) O(n)
Add/Remove in the interior O(n) O(n) O(n)
Resize O(n) N/A N/A
Find By position O(1) O(1) O(n)
Find By value O(n) O(n) O(n)

Dynamic arrays

Dynamic arrays are the next logical extension of arrays.

Associative Array

Associative arrays, also called maps or dictionaries, are an abstract data type that can hold data in (key, value) pairs.

Function Functionality
insert(key, value) Add a (key, value) pair to the associative array
remove(key) Remove the key’s pair in the associative array
update(key, value) Assigns/updates the value to/of the existing key
lookup(key) Returns the value assigned to this key

Time Complexity

Function Array Red-Black Tree Hash Table
insert O(n) O(log(n)) O(1)
remove O(n) O(log(n)) O(1)
update O(n) O(log(n)) O(1)
lookup O(n) O(log(n)) O(1)

Linked list

Types of Linked List

  • Simple Linked List − Item navigation is forward only.
  • Doubly Linked List − Items can be navigated forward and backward.
  • Circular Linked List − Last item contains link of the first element as next and the first element has a link to the last element as previous.

Hash tables

They’re also known as hash maps, maps, dictionaries,and associative arrays.

Python has hash tables; they’re called dictionaries.

>>> phone_book = {}
Same as phone_book = dict()

Alt text

Binary Search Tree

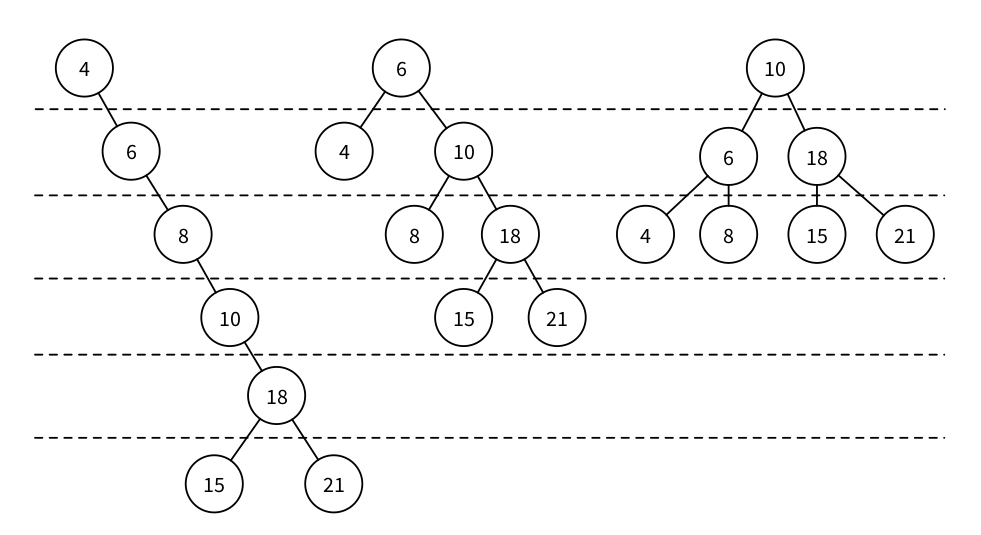
A Binary Search Tree is a special type of Tree that can be efficiently searched. Nodes in Binary Search Trees can have at most two chil- dren. And nodes are positioned according to their value/key. Children nodes to the left of the parent must be smaller than the parent, children nodes to the right must be greater.

Tree Balancing

If we insert too many nodes in a Binary Search Tree, we end up with a tree of very high height, where many nodes have only one child. But we can rearrange nodes in a tree such that its height is reduced. This is called tree balancing . A perfectly balanced tree has the minimum possible height.

Alt text

The Red-Black Tree

The Red-Black Tree is a famous example of a self-balancing tree, which colors nodes either “red” or “black” for its balancing strat- egy.

The AVL Tree

The AVL Tree is another breed of self-balancing trees. They require a bit more time to insert and delete items than Red-Black Trees, but tend to have better balancing. This means they’re faster than Red-Black Trees for retrieving items. AVL Trees are often used to optimize performance in read-intensive scenarios.

The Binary Heap

The Binary Heap is a special type of Binary Search Tree, in which we can find the smallest (or highest) item instantly. This data structure is especially useful for implementing Priority Queues. In the Heap it costs O(1) to get the minimum (or maximum) item, be- cause it is always the Root Node of the tree. Searching or inserting nodes still costs O( log n) . It has the same node placement rules as the Binary Search Tree, plus an extra restriction: a parent node must be greater (or smaller) than both its child nodes.

Alt text

The Graph

The Graph is similar to the Tree. The difference is that there’s no children or parent nodes, and therefore, no Root Node. For example, graphs are ideal for representing a social network, where nodes are people and edges represent friendships.

Types of Graphs

  • Undirected Graph - A undirected graph contains edges but the edges are not directed ones.
  • Directed Graph - In a directed graph, each edge has a direction.
  • Weighted Graphs - edges has weight to represent an value

Rerpresenting Graphs

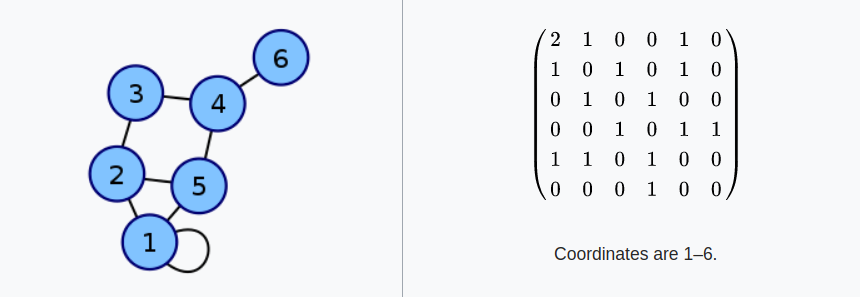
an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.

Alt text

Tree

A tree in an undirectect graph with no cycles.

The algorithm to solve a shortest-path problem is called breadth-first search.

Each graph is made up of nodes and edges. (A) —edge—> (B) A and B are neighbors

• Question type 1: Is there a path from node A to node B? • Question type 2: What is the shortest path from node A to node B?

Graphs

Graph Implementations

Edge lists

One simple way to represent a graph is just a list, or array, of E ∣E∣vertical bar, E, vertical bar edges, which we call an edge list. To represent an edge, we just have an array of two vertex numbers, or an array of objects containing the vertex numbers of the vertices that the edges are incident on

Alt text

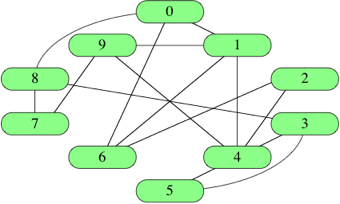
[ [0,1], [0,6], [0,8], [1,4], [1,6], [1,9], [2,4], [2,6], [3,4], [3,5],
[3,8], [4,5], [4,9], [7,8], [7,9] ]

Adjacency Matrix

For a graph with V ∣V∣vertical bar, V, vertical bar vertices, an adjacency matrix is a V \times V ∣V∣×∣V∣vertical bar, V, vertical bar, times, vertical bar, V, vertical bar matrix of 0s and 1s, where the entry in row i ii and column j jj is 1 if and only if the edge (i,j) (i,j)left parenthesis, i, comma, j, right parenthesis is in the graph.

Alt text

Directed Graph Unweighted graph boolean Weighted graph values

Adjacency List

Representing a graph with adjacency lists combines adjacency matrices with edge lists. For each vertex i ii, store an array of the vertices adjacent to it. We typically have an array of V ∣V∣vertical bar, V, vertical bar adjacency lists, one adjacency list per vertex.

Alt text

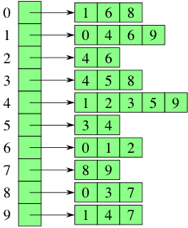
In JavaScript, we represent these adjacency lists by:

[ [1, 6, 8],
  [0, 4, 6, 9],
  [4, 6],
  [4, 5, 8],
  [1, 2, 3, 5, 9],
  [3, 4],
  [0, 1, 2],
  [8, 9],
  [0, 3, 7],
  [1, 4, 7] ]

Graph Traversals

Depth First Search (DFS)

Depth First Search (DFS) algorithm traverses a graph in a depthward motion and uses a stack to remember to get the next vertex to start a search, when a dead end occurs in any iteration.

Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Push it in a stack. Rule 2 − If no adjacent vertex is found, pop up a vertex from the stack. (It will pop up all the vertices from the , which do not have adjacent vertices.) Rule 3 − Repeat Rule 1 and Rule 2 until the stack is empty.

Breadth First Search (BFS)

Breadth First Search (BFS) algorithm traverses a graph in a breadthward motion and uses a queue to remember to get the next vertex to start a search, when a dead end occurs in any iteration.

Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Insert it in a queue. Rule 2 − If no adjacent vertex is found, remove the first vertex from the queue. Rule 3 − Repeat Rule 1 and Rule 2 until the queue is empty.

Dijkstra’s algorithm

Tree

Tree represents the nodes connected by edges.

Alt text

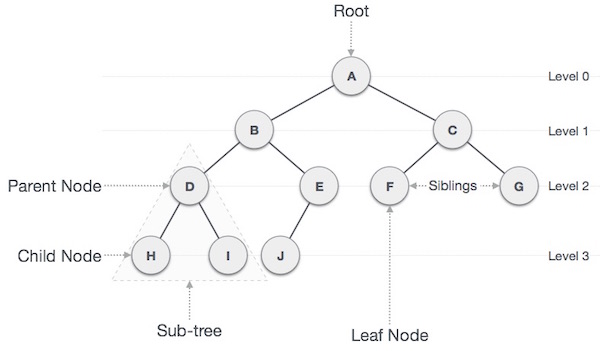
every tree have n nodes n-1 edges

Binary Search Tree

A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties −

The left sub-tree of a node has a key less than or equal to its parent node’s key.

The right sub-tree of a node has a key greater than to its parent node’s key.

https://www.youtube.com/playlist?list=PLDV1Zeh2NRsDGO4–qE8yH72HFL1Km93P

References

Tags: algorithms · computer-science · data-structure Previous Post: Algorithms Next Post: State Machines

Recent Posts