State Machines
2 April 2018 · Filed in TutorialTheory of Computation
- Regular Languages
- Regular Expressions
- Finite State Machine
Determinism
Deterministic Given the current state, we know what the next state will be.
- In DFA, given the current state we know what the next state will be
- It has only one unique next state
- It has no choices or randomness
- It is simple and easy to design
Nondeterminism
Nondeterministic Given the current state, there may be multiple next states.
- In NFA, given the current state there could be multiple next states
- The next state may be chosen at random
- All the next states may be chosen in parrallel
Regular Languages
A language is a Regular Language if some Finit State Machine recognizes it.
What language are not regular?
- Anything that requires memory
- Languages are not recognized by any FSM
Regular Expression
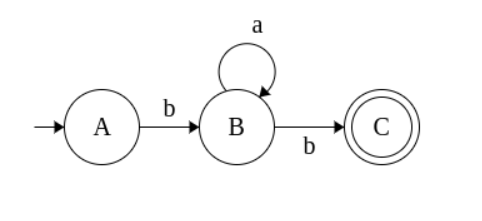
- ba*b -> bb,bab,baab,…
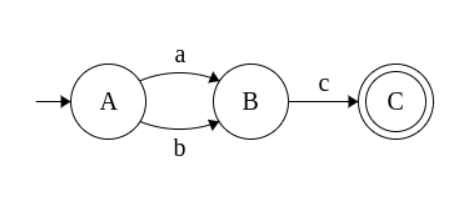
- (a+b)c -> ac,bc
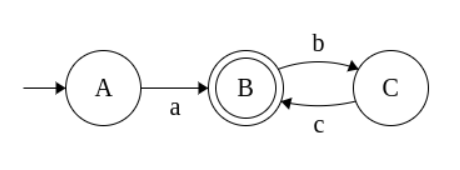
- a(ab)* -> a,abc,abcbc,abcbcbc,…
Regular Grammar
| Grammar Type | Grammar Accepted | Language Accepted | Automatan |
|---|---|---|---|
| 0 | Unrestricted Grammar | Recursively Enumerable Language | Turing Machine |
| 1 | Context Sensitive Grammar | Sensitive Language | Linear Bounded Automaton |
| 2 | Context Free Grammar | Context Free Language | Pushdown Automaton |
| 3 | Regular Grammar | Regular Language | Finite State Automata |
Finite State Machine (FSM)
Classes of automata A finite-state machine (FSM) or finite-state automaton , finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some external inputs; the change from one state to another is called a transition. An FSM is defined by a list of its states, its initial state, and the conditions for each transition. Finite state machines are of two types
- deterministic finite state machines
-
non-deterministic finite state machines
- Memory if FSM is very limited
- It cannot store or count strings
Example
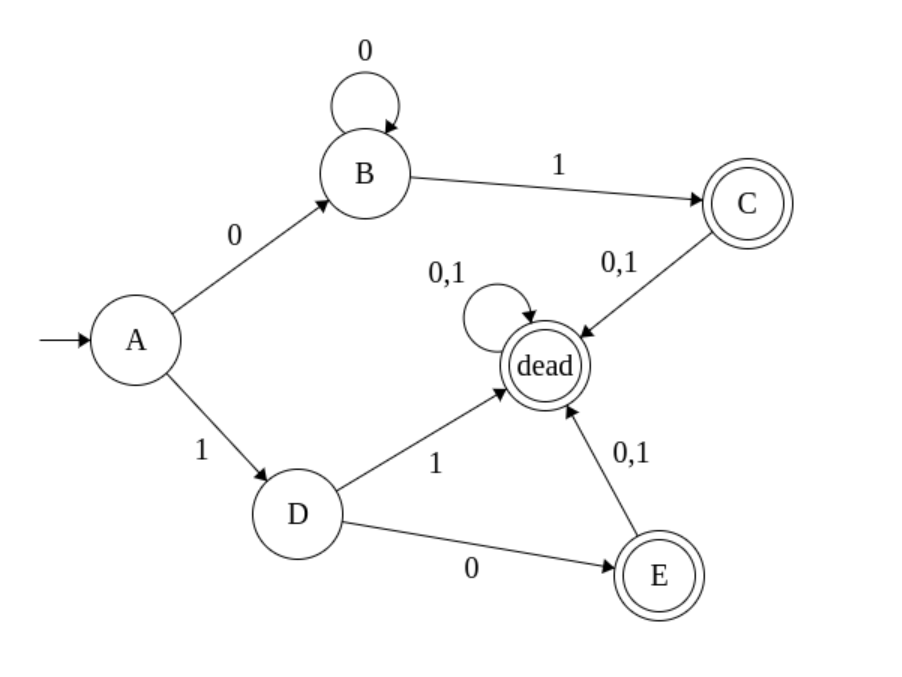 Recognizes 10
also 01,001,0001,..0+1
Recognizes 10
also 01,001,0001,..0+1
- States(Nodes)
- Transitions (Edges)
- Starting State
- Excepting State (final)
Alpahabet of Symbols Σ = {0, 1}
- Start in starting state
- Start at first symbol in the string
- Follow transition as determined by symbol in the string
- Process all symbols in string
- Do you end up in an accepting state or not ?
- The set of string that are accepted?
- Other are Rejeted
Finite Automata
with output
- Moore Machine
- Mealy Machine
without output
- DFA
- NFA
- -NFA
Deterministic Finite Automata (DFA)
A deterministic finite state automaton (DFSA)—is a finite-state machine that accepts and rejects strings of symbols and only produces a unique computation (or run) of the automaton for each input string.
The following example is of a DFA M, with a binary alphabet, which requires that the input contains an even number of 0s.
The state diagram for M
M = (Q, Σ, δ, q0, F)
Q = {S1, S2},
Σ = {0, 1},
q0 = S1,
F = {S1}, and
δ is defined by the following state transition table:
| state | 0 | 1 |
|---|---|---|
| S1 | S2 | S1 |
| S2 | S1 | S2 |
Q = set of all states Σ = inputs (Alphabet, finit set of symbols) q0 = start state (initial state) q0 ∈ Q F = set of final states F ⊆ Q δ = the transition function QxΣ -> Q
Nondeterministic Finite Automata (DFA)
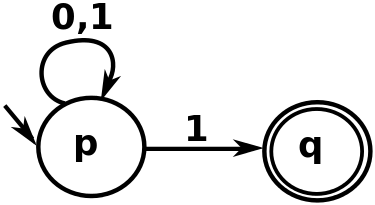
Let M be an NFA, with a binary alphabet, that determines if the input ends with a 1.
| Input/State | 0 | 1 |
|---|---|---|
| p | {p} | {p,q} |
| q | ∅ | ∅ |
if there is any way to run the machine that ends in any set of states out of which atleast one state is a final, then the NFA accepts
Example 1
Set of all string that start with 0
L = {0,00,01,000,…0}
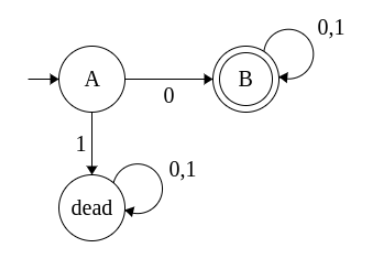
Example 2
Construct a NFA that accepts sets of all strings over {0,1}
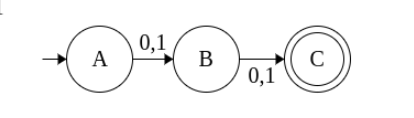
Example 3
L = { Set of all strings that ends with ‘1’}
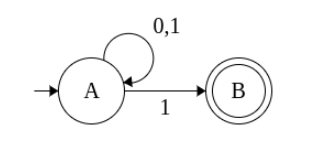
Example 4
L = { Set of all strings that contain ‘0’}
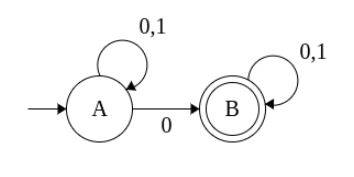
Example 5
L = { Set of all strings that starts with ‘10’}

Example 6
L = { Set of all strings that contain ‘01’}
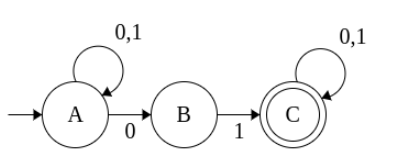
Example 7
L = { Set of all strings that ends with ‘11’}
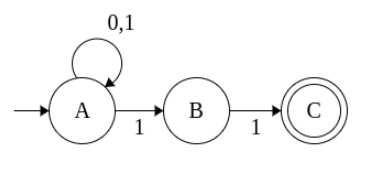
Finit Automata With Outputs
Mealy machine
In the theory of computation, a Mealy machine is a finite-state machine whose output values are determined both by its current state and the current inputs.
A Mealy machine is a 6-tuple (S,S,Σ,Λ,T,G) consisting of the following:
- a finite set of states S
- a start state S0 which is an element of S
- a finite set called the input alphabet Σ
- a finite set called the output alphabet Λ
- a transition function T : S x Σ -> S mapping pairs of a state and an input symbol to the corresponding next state.
- an output function G : S x Σ -> Λ mapping pairs of a state and an input symbol to the corresponding output symbol.
Example 1
Construct a Mealy Machine that prints ‘a’ whenever the sequence ‘01’ is encountered in any input binary string.
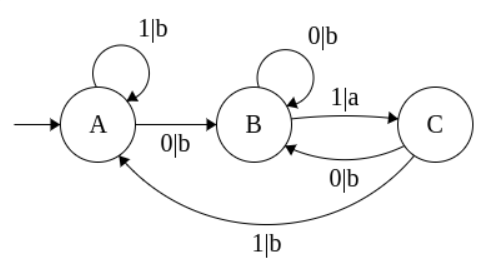
Σ = {0,1} - input Λ = {a,b} - print
0110 -> babb 1000 -> bbbb
Moore machine
In the theory of computation, a Moore machine is a finite-state machine whose output values are determined only by its current state.
A Moore machine can be defined as a 6-tuple (S,S,Σ,Λ,T,G) consisting of the following:
- a finite set of states S
- a start state S0 which is an element of S
- a finite set called the input alphabet Σ
- a finite set called the output alphabet Λ
- a transition function T : S x Σ -> S mapping a state and the input alphabet to the next state
- an output function G : S -> Λ mapping each state to the output alphabet
Example 1
Construct a Moore Machine that prints ‘a’ whenever the sequence ‘01’ is encountered in any input binary string.
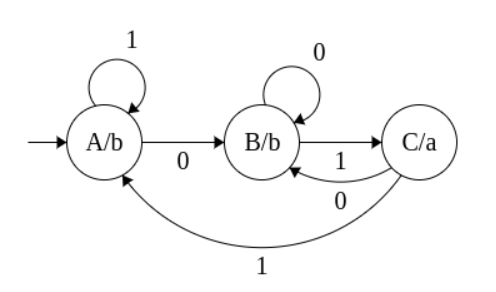
0110 -> babb 0101 -> baba
Context Free Language (CFL)
Turning Machine
Undecidabe
https://en.wikipedia.org/wiki/Deterministic_finite_automaton
https://www.youtube.com/watch?v=6veoK7DRv_w&list=PLbtzT1TYeoMjNOGEiaRmm_vMIwUAidnQz&index=3
https://www.youtube.com/watch?v=Bcen1W_uFEU&index=13&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev
Tags: state-machines Previous Post: Data Structure Next Post: Java Swing
