26 Jun 2018
author: teymur
comments: true
date: 2019-04-09 00:00:00+00:00
layout: post
slug: gradle
title: Java Gradle
categories: Tutorial
published: false
tags:
task - self contain unite of work
task can depond from another tasks
gradle task –all
gradle demon - demon process
gradle build script - gradle dsl
Groovy
22 Apr 2018
author: teymur
comments: true
date: 2019-04-09 00:00:00+00:00
layout: post
slug: java-swing
title: Java Swing
categories: Tutorial
published: false
tags:
Swing The Model View Controller
-
Model The model encompasses the state data for each component. There are different models for different types of components. For example, the model of a scrollbar component might contain information about the current position of its adjustable “thumb,” its minimum and maximum values, and the thumb’s width (relative to the range of values). A menu, on the other hand, may simply contain a list of the menu items the user can select from. This information remains the same no matter how the component is painted on the screen; model data is always independent of the component’s visual representation.
-
View The view refers to how you see the component on the screen. For a good example of how views can differ, look at an application window on two different GUI platforms. Almost all window frames have a title bar spanning the top of the window. However, the title bar may have a close box on the left side (like the Mac OS platform), or it may have the close box on the right side (as in the Windows platform). These are examples of different types of views for the same window object.
-
Controller The controller is the portion of the user interface that dictates how the component interacts with events. Events come in many forms e.g., a mouse click, gaining or losing focus, a keyboard event that triggers a specific menu command, or even a directive to repaint part of the screen. The controller decides how each component reacts to the eventif it reacts at all.
MVC in Swing
Swing actually uses a simplified variant of the MVC design called the model-delegate.
This design combines the view and the controller object into a single element, the UI delegate, which draws the component to the screen and handles GUI events
Internal Frame
Same functions as a normal Frame object, but confined to the visible area of the container it is placed in
Actions
Swing containers, such as JMenu, JPopupMenu, and JToolBar, can each accept action
objects with their add( ) methods. When an action is added, these containers automatically
create a GUI component, which the add( ) method then returns to you for customization.
For example, a JMenu or a JPopupMenu creates and returns a JMenuItem from an Action
while a JToolBar creates and returns a JButton. The action is then paired with the newly
created GUI component in two ways: the GUI component registers as a
PropertyChangeListener for any property changes that might occur in the action object,
while the action object registers as an ActionListener on the GUI component. Figure 3-1
shows the interactions between a menu item or toolbar and an Action.
Essentially, this means that if the menu item or button is selected by the user, the functionality inside the action is invoked. On the other hand, if the action is disabled, it sends a PropertyChangeEvent to both the menu item and the toolbar, causing them to disable and turn gray. Similarly, if the action’s icon or name is changed, the menu and toolbar are automatically updated.
The Action Interface
An action is defined by the interface it implements, in this case javax.swing.Action.
Action extends the ActionListener interface from AWT; this forces concrete classes
that implement Action to provide an actionPerformed( ) method. The programmer
uses the actionPerformed( ) method to implement whatever behavior is desired. For
example, if you are creating a Save action, you should put the code that saves the data inside of your actionPerformed( ) method.
Events
Objects implementing the Action interface must fire a PropertyChangeEvent when any
keyed property is changed, or when the action is enabled or disabled. Containers that accept actions typically listen for these PropertyChangeEvent notifications so they can update their own properties or appearances.
public abstract void addPropertyChangeListener(PropertyChangeListener listener)
public abstract void removePropertyChangeListener(PropertyChangeListener listener)
Add or remove the specified PropertyChangeListener from the event listener list
The AbstractAction Class
The AbstractAction class is an abstract implementation of the Action interface.
AbstractAction provides the default functionality for almost all methods in the Action
interface.
Graphical Interface Events
Whenever you interact with your application’s user interface, the application receives an event
from the windowing system to let it know that something happened. Some events come from
the mouse, such as mouse clicks, mouse movements, and mouse drags
Graphics Environments
You can retrieve that information for your own code through the GraphicsEnvironment, GraphicsDevice,
and GraphicsConfiguration classes from the java.awt package. While they aren’t
part of Swing proper, these classes are definitely useful for Swing applications, especially
those that take full advantage of their environment.
To sum up these classes, a system keeps a local GraphicsEnvironment object that
describes the devices on the system with an array of GraphicsDevice objects. Each
GraphicsDevice contains (or at least may contain) multiple configurations of device
capabilities (such as pixel formats or which visual screen you’re on) bundled up in an array of
GraphicsConfiguration objects.
Headless Modes
One other variation on the graphics environment is “headless” operation. This mode of running
without any monitor shows up quite often on back-end systems. Java servlets trying to use the
AWT, 2D, and Swing classes to draw dynamic graphs for a web page are a classic example of
applications that need a graphics environment on a machine that might not have any graphics
displays. You can detect such a case with the GraphicsEnvironment.isHeadless( )
call
Sending Change Events in Swing
Swing uses two different change event classes. The first is the standard
java.beans.PropertyChangeEvent class. This class passes a reference to the
object, sending the change notification as well as the property name, its old value, and its new
value. The second, javax. swing.event.ChangeEvent, is a lighter version that
passes only a reference to the sending objectin other words, the name of the property that
changed, as well as the old and new values, are omitted.
The JComponent Class
JComponent is an abstract class that almost all Swing components extend; it provides much
of the underlying functionality common throughout the Swing component library. Just as the
java.awt.Component class serves as the guiding framework for most of the AWT
components, the javax.swing.JComponent class serves an identical role for the Swing
components. We should note that the JComponent class extends java.awt.Container
(which in turn extends java.awt.Component), so it is accurate to say that Swing
components carry with them a great deal of AWT functionality as well.
Because JComponent extends Container, many Swing components can serve as
containers for other AWT and Swing components. These components may be added using the
traditional add( ) method of Container. In addition, they can be positioned with any Java
layout manager while inside the container.
Inherited Properties
Swing components carry with them several properties that can be accessed through
JComponent but otherwise originate with AWT. Before we go any further, we should review
those properties of java.awt.Container and java.awt.Component that can be used
to configure all Swing components.
Let’s discuss these properties briefly. The background and foreground properties
indicate which colors the component uses to paint itself. We should mention that with Swing the
background property is disabled if the component is transparent (not opaque). The readonly
colorModel property returns the current model used to translate colors to pixel values;
generally, the user does not need to access this property. The font property lets you get or
set the font used for displaying text in the component.
The indexed component property maintains a list of all the components inside the container.
You can tell how many there are with the integer componentCount property. If you want to
access all of them through a Component array, retrieve the components property. The
insets property specifies the current insets of the container, while the layout property
indicates which layout manager is managing the components of the container. Technically, this
means that you can use any component as a container. Don’t be misled; if a component doesn’t
seem like a reasonable container, it probably can’t be used as one. (Don’t, for example, try to
add a JButton to a JScrollBar.) A number of components use these properties for
internal, specialized layout managers and components.
The locale property specifies the internationalization locale for the application. The
location property indicates the x,y coordinates of the component’s upper-left corner in the
container’s coordinate space. If you want to see the location of the component’s upper-left
corner in screen coordinates, use the read-only locationOnScreen property.
The name property gives this component a string-based name that components can display if
they choose. The parent property references the container that is acting as this component’s
parent, or null if there is none. The size property specifies the component’s current height
and width in pixels.
The showing property indicates whether the component is currently showing on the screen,
while the visible property tells if the component is marked to be drawn on the screen.
There’s an odd, nonintuitive relationship between visible and showing. A component that
is visible isn’t necessarily showing. “Visible” means that a component is capable of being
displayed; “showing” means that the component is actually displayed (though it may be
obscured by something else). Most containers (JPanel, JFrame, etc.) are invisible by
default; most other components (JButton, etc.) are visible by default. So if you add a
JButton to an invisible JFrame, for example, the button is visible but not showing. It can be
displayed but happens to be in a container that isn’t currently displayed.
Finally, if the valid property is false, the component needs to be resized or moved by the
component’s layout manager. If it is true, the component is ready to be displayed.
UI Delegates and UIClassIDs
Each Swing component maintains a read-only string constant, UIClassID, that identifies the
type of UI delegate that it uses. Most Swing components override the accessor
getUIClassID( ) and return a string constant, typically the letters “UI” appended to the
name of the component (without the “J”).
Adding Borders
It’s easy to add borders to Swing components, a feature AWT lacks. The JComponent
border property accepts objects that implement the javax.swing.border.Border
interface.
JLabel label = new JLabel(“A Simple Label”);
label.setBorder(BorderFactory.createEtchedBorder( ));
JComponent also provides Swing components with support for tooltips. Tooltips are small
windows of text that pop up when the user rests the mouse over the target component.
JButton button = new JButton(“Press Me!”); // JButton extends JComponent.
button.setToolTipText(“Go Ahead!”);
System.out.println(button.getToolTipText( ));
The JPanel Class
JPanel is an extension of JComponent (which, remember, extends
java.awt.Container) used for grouping together other components. It gets most of its
implementation from its superclasses. Typically, using JPanel amounts to instantiating it,
setting a layout manager (this can be set in the constructor and defaults to a FlowLayout),
and adding components to it using the add( ) methods inherited from Container.
The JRootPane Class
JRootPane is a special container that extends JComponent and is used by many of the
other Swing containers. It’s quite different from most containers you’re probably used to using. The first thing to understand about JRootPane is that it contains a fixed set of components: aComponent called the glass pane and a JLayeredPane called, logically enough, the layered pane. Furthermore, the layered pane contains two more components: a JMenuBar and a Container called the content pane.
The glass pane
Hidden, by default. If you make the glass pane visible, then it’s like a sheet of glass over all the other parts of the root pane. It’s completely transparent unless you implement the glass pane’s paintComponent method so that it does something, and it can intercept input events for the root pane.
The layered pane
Serves to position its contents, which consist of the content pane and the optional menu bar. Can also hold other components in a specified Z order.
The content pane
The container of the root pane’s visible components, excluding the menu bar.
The optional menu bar
The home for the root pane’s container’s menus. If the container has a menu bar, you generally use the container’s setJMenuBar method to put the menu bar in the appropriate place.
02 Apr 2018
Theory of Computation
- Regular Languages
- Regular Expressions
- Finite State Machine
Determinism
Deterministic Given the current state, we know what the next state will be.
- In DFA, given the current state we know what the next state will be
- It has only one unique next state
- It has no choices or randomness
- It is simple and easy to design
Nondeterminism
Nondeterministic Given the current state, there may be multiple next states.
- In NFA, given the current state there could be multiple next states
- The next state may be chosen at random
- All the next states may be chosen in parrallel
Regular Languages
A language is a Regular Language if some Finit State Machine recognizes it.
What language are not regular?
- Anything that requires memory
- Languages are not recognized by any FSM
Regular Expression
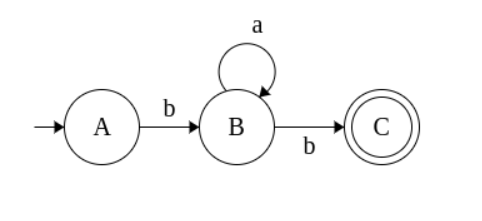
- ba*b -> bb,bab,baab,…
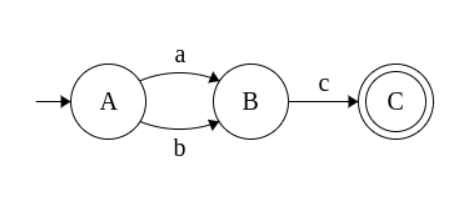
- (a+b)c -> ac,bc
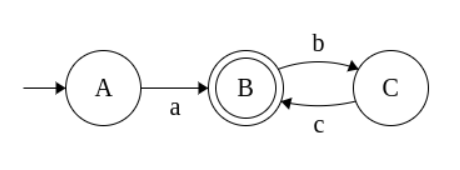
- a(ab)* -> a,abc,abcbc,abcbcbc,…
Regular Grammar
| Grammar Type |
Grammar Accepted |
Language Accepted |
Automatan |
| 0 |
Unrestricted Grammar |
Recursively Enumerable Language |
Turing Machine |
| 1 |
Context Sensitive Grammar |
Sensitive Language |
Linear Bounded Automaton |
| 2 |
Context Free Grammar |
Context Free Language |
Pushdown Automaton |
| 3 |
Regular Grammar |
Regular Language |
Finite State Automata |
Finite State Machine (FSM)
Classes of automata A finite-state machine (FSM) or finite-state automaton , finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some external inputs; the change from one state to another is called a transition.
An FSM is defined by a list of its states, its initial state, and the conditions for each transition.
Finite state machines are of two types
Example
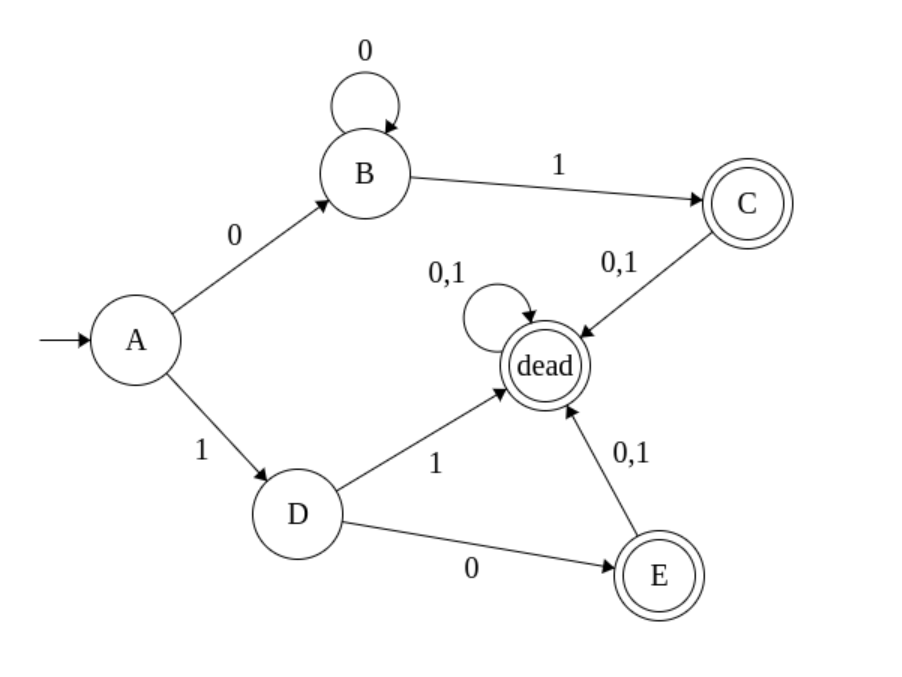 Recognizes 10
also 01,001,0001,..0+1
Recognizes 10
also 01,001,0001,..0+1
- States(Nodes)
- Transitions (Edges)
- Starting State
- Excepting State (final)
Alpahabet of Symbols Σ = {0, 1}
- Start in starting state
- Start at first symbol in the string
- Follow transition as determined by symbol in the string
- Process all symbols in string
- Do you end up in an accepting state or not ?
- The set of string that are accepted?
- Other are Rejeted
Finite Automata
with output
- Moore Machine
- Mealy Machine
without output
Deterministic Finite Automata (DFA)
A deterministic finite state automaton (DFSA)—is a finite-state machine that accepts and rejects strings of symbols and only produces a unique computation (or run) of the automaton for each input string.
The following example is of a DFA M, with a binary alphabet, which requires that the input contains an even number of 0s.

The state diagram for M
M = (Q, Σ, δ, q0, F)
Q = {S1, S2},
Σ = {0, 1},
q0 = S1,
F = {S1}, and
δ is defined by the following state transition table:
| state |
0 |
1 |
| S1 |
S2 |
S1 |
| S2 |
S1 |
S2 |
Q = set of all states
Σ = inputs (Alphabet, finit set of symbols)
q0 = start state (initial state) q0 ∈ Q
F = set of final states F ⊆ Q
δ = the transition function QxΣ -> Q
Nondeterministic Finite Automata (DFA)
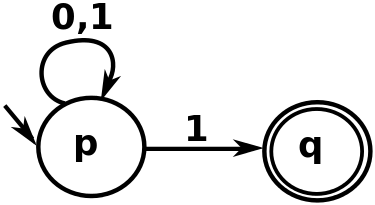
Let M be an NFA, with a binary alphabet, that determines if the input ends with a 1.
| Input/State |
0 |
1 |
| p |
{p} |
{p,q} |
| q |
∅ |
∅ |
if there is any way to run the machine that ends in any set of states out of which
atleast one state is a final, then the NFA accepts
Example 1
Set of all string that start with 0
L = {0,00,01,000,…0}
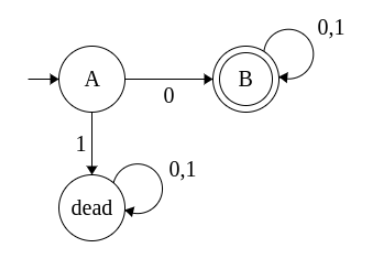
Example 2
Construct a NFA that accepts sets of all strings over {0,1}
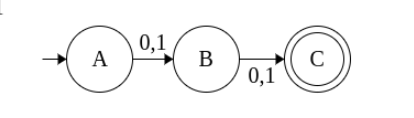
Example 3
L = { Set of all strings that ends with ‘1’}
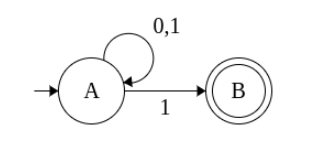
Example 4
L = { Set of all strings that contain ‘0’}
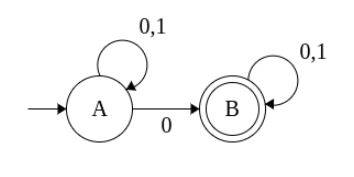
Example 5
L = { Set of all strings that starts with ‘10’}

Example 6
L = { Set of all strings that contain ‘01’}
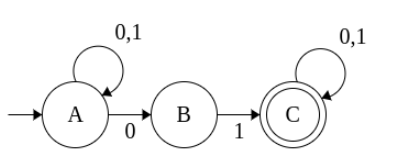
Example 7
L = { Set of all strings that ends with ‘11’}
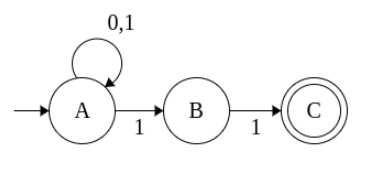
Finit Automata With Outputs
Mealy machine
In the theory of computation, a Mealy machine is a finite-state machine whose output values are determined both by its current state and the current inputs.
A Mealy machine is a 6-tuple (S,S,Σ,Λ,T,G) consisting of the following:
- a finite set of states S
- a start state S0 which is an element of S
- a finite set called the input alphabet Σ
- a finite set called the output alphabet Λ
- a transition function T : S x Σ -> S mapping pairs of a state and an input symbol to the corresponding next state.
- an output function G : S x Σ -> Λ mapping pairs of a state and an input symbol to the corresponding output symbol.
Example 1
Construct a Mealy Machine that prints ‘a’ whenever the sequence ‘01’ is encountered in any input binary string.
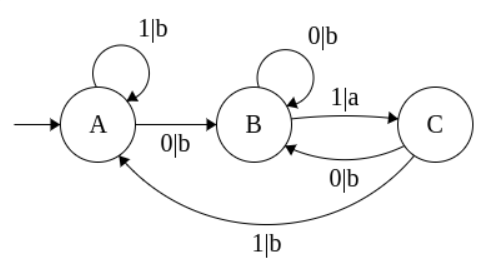
Σ = {0,1} - input
Λ = {a,b} - print
0110 -> babb
1000 -> bbbb
Moore machine
In the theory of computation, a Moore machine is a finite-state machine whose output values are determined only by its current state.
A Moore machine can be defined as a 6-tuple (S,S,Σ,Λ,T,G) consisting of the following:
- a finite set of states S
- a start state S0 which is an element of S
- a finite set called the input alphabet Σ
- a finite set called the output alphabet Λ
- a transition function T : S x Σ -> S mapping a state and the input alphabet to the next state
- an output function G : S -> Λ mapping each state to the output alphabet
Example 1
Construct a Moore Machine that prints ‘a’ whenever the sequence ‘01’ is encountered in any input binary string.
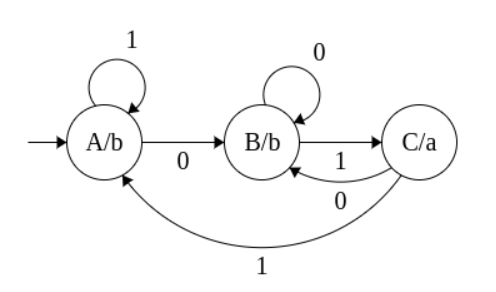
0110 -> babb
0101 -> baba
Context Free Language (CFL)
Turning Machine
Undecidabe
https://en.wikipedia.org/wiki/Deterministic_finite_automaton
https://www.youtube.com/watch?v=6veoK7DRv_w&list=PLbtzT1TYeoMjNOGEiaRmm_vMIwUAidnQz&index=3
https://www.youtube.com/watch?v=Bcen1W_uFEU&index=13&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev
28 Mar 2018
Abstract Data Type
An Abstract Data Type (ADT) is the specification of a group of
operations that make sense for a given data type.
Primitive data types
Primitive data types are those with built-in support in the programming language you’re using—they work without external modules.
These always include integers, floating points, 3 and generic operations with them (addition, subtraction, division).
Structures
An Abstract Data Type only describes how variables of a given data type are operated. It provides a list of operations, but doesn’t explain how data operations happen. Conversely, data structures
describe how data is to be organized and accessed in the computer’s memory. They provide ways for implementing ADTs in
data-handling modules.
Abstract Data Types
| Abstract Data Type |
Other Common Names |
Commonly Implemented With |
| List |
Sequence |
Array,Linked List |
| Queue |
|
Array,Linked List |
| Double Ended Queue |
Equeue, Deque |
Array,Doubly Linked List |
| Stack |
|
Array,Linked List |
| Associative Array |
Dictionary, Hash Map, Hash, Map |
Hash Table |
| Set |
|
Red-Black Tree,Hash Table |
| Priority Queue |
Heap |
Heap |
Container
List
Set
Multiset
Map
Multimap
Graph
Stack
Queue
Priority queue
Double-ended queue
Double-ended priority queue
Linear Data Structures
Hash-Based Data Structures
Trees
Binary Search Trees
Heaps
Graphs
Strings
Lists
A list is an abstract data type used for storing sequential items
The head is the first item in the list.
The tail is all remaining items.
The tail is itself a list, having its own head and tail:
| Function |
Functionality |
| new |
Creates an empty list. |
| append |
Adds an item to the end of the list. |
| prepend |
Adds an item to the beginning of the list. |
| head |
Returns the item at the beginning of the list. |
| tail |
Returns all items except the head. If the list only has 1 item, returns an empty list. |
| is_empty |
Returns a bool indicating whether or not the list contains any items. |
Stack
Stack can be implemented with a variety of data structures, such as a linked list or an array
LIFO data structure. LIFO stands for Last-in-first-out.
| Function |
Functionality |
| push(i) |
Insert element i at the top of the stack. |
| pop() |
Remove the element at the top of the stack. |
| peek() |
returns the element at the top of the stack without changing the stack |
| size() |
returns the current size of the stack |
| isFull() |
check if stack is full. |
| isEmpty() |
check if stack is empty. |
Time Complexity
| Function |
Linked list |
Array |
| push() |
O(1) |
O(1) |
| pop() |
O(1) |
O(1) |
Queue
Queue is an abstract data structure, somewhat similar to Stacks. Unlike stacks, a queue is open at both its ends. One end is always used to insert data (enqueue) and the other is used to remove data (dequeue).
Queue follows First-In-First-Out methodology, i.e., the data item stored first will be accessed first.
| Function |
Functionality |
| enqueue(i) |
Insert element i at the tail of the queue. |
| dequeue() |
Remove the element at the head of the queue. |
| peek() |
returns the element at the head of the queue without changing the queue. |
| size() |
returns the current size of the queue |
| isfull() |
Checks if the queue is full. |
| isempty() |
Checks if the queue is empty. |
Time Complexity
| Function |
Linked list |
Array |
| enqueue() |
O(1) |
O(n) |
| dequeue() |
O(1) |
O(n) |
Double Ended Queues
Double ended queues, called deques for short, are a generalized form of the queue. It is exactly like a queue except that elements can be added to or removed from the head or the tail
| Function |
Functionality |
| append(i) |
Adds element i to the tail of the queue |
| prepend(i) |
Adds element i to the head of the queue |
| delete_last() |
Removes the element at the tail of the queue |
| delete_first() |
Removes the element at the head of the queue |
| examine_last() |
Returns the element at the tail of the queue |
| examine_first() |
Returns the element at the head of the queue |
Time Complexity
| Operation |
Doubly Linked List |
Dynamic Array |
| append |
O(1) |
O(1) |
| prepend |
O(1) |
O(n) |
| delete_last |
O(1) |
O(1) |
| delete_first |
O(1) |
O(n) |
| examine_last |
O(1) |
O(1) |
| examine_first |
O(1) |
O(1) |
Priority Queue
Priority queues are a kind of abstract data type that generalizes the queue. Their principles are exactly the same except that they also include a priority for every value in the queue. When a value is inserted, a priority is assigned to it. The value with the highest priority is always removed first.
| Function |
Functionality |
| insert(i, p) |
Add value i with priority p. |
| pop() |
Remove and return the element with the highest priority. |
| peek() |
Return the element with the highest priority without changing the queue. |
Time Complexity
| Function |
Heap |
| insert(i, p) |
O(logn) |
| pop() |
O(logn) |
| peek() |
O(1) |
Sets
Sets are a type of abstract data type that allows you to store a list of non-repated values. Their name derives from the mathematical concept of finite sets.
Unlike an array, sets are unordered and unindexed
These are the two properties of a set: the data is unordered and it is not duplicated.
| Function |
Functionality |
| insert(i) |
Adds i to the set |
| remove(i) |
Removes i from the set |
| size() |
Returns the size of the set |
| contains(i) |
Returns whether or not the set contains i |
| union(S, T) |
Returns the union of set S and set T |
| intersection(S, T) |
Returns the intersection of set S and set T |
| difference(S, T) |
Returns the difference of set S and set T |
| subset(S, T) |
Returns whether or not set S is a subset of set T |
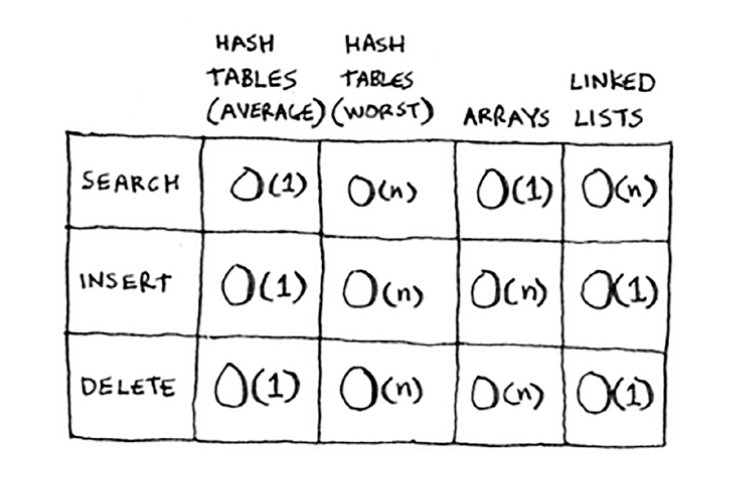
Time Complexity
A hash table is the most common data structure
| Function |
Hash table |
| insert() |
O(1) |
| contains() |
O(1) |
| remove() |
O(1) |
Array
The array is a basic abstract data type that holds an ordered collection of items accessible by an integer index. These items can be anything from primitive types such as integers to more complex types like instances of classes. Since it’s an ADT, it doesn’t specify an implementation, but is almost always implemented by an array (data structure) or dynamic array.
They are extremely ubiquitous and among the oldest, most widely used data structures in programming.
Unless otherwise specified, for the remainder of this wiki, the word “array” will refer to the data structure and not the abstract data type.
Arrays are often used to implement abstract data types such as arrays (ADT) and stacks.
In Java, you can create an array of any primitive data type, abstract data type, or custom class. Java also provides an ArrayList type which gives you more flexibility.
Following are the basic operations supported by an array.
- Traverse − print all the array elements one by one.
- Insertion − Adds an element at the given index.
- Deletion − Deletes an element at the given index.
- Search − Searches an element using the given index or by the value.
- Update − Updates an element at the given index.
| Operation |
Array |
ArrayList |
Linked List |
| Read |
O(1) |
O(1) |
O(n) |
| Add/Remove at end |
O(1) |
O(1) |
O(n) |
| Add/Remove in the interior |
O(n) |
O(n) |
O(n) |
| Resize |
O(n) |
N/A |
N/A |
| Find By position |
O(1) |
O(1) |
O(n) |
| Find By value |
O(n) |
O(n) |
O(n) |
Dynamic arrays
Dynamic arrays are the next logical extension of arrays.
Associative Array
Associative arrays, also called maps or dictionaries, are an abstract data type that can hold data in (key, value) pairs.
| Function |
Functionality |
| insert(key, value) |
Add a (key, value) pair to the associative array |
| remove(key) |
Remove the key’s pair in the associative array |
| update(key, value) |
Assigns/updates the value to/of the existing key |
| lookup(key) |
Returns the value assigned to this key |
Time Complexity
| Function |
Array |
Red-Black Tree |
Hash Table |
| insert |
O(n) |
O(log(n)) |
O(1) |
| remove |
O(n) |
O(log(n)) |
O(1) |
| update |
O(n) |
O(log(n)) |
O(1) |
| lookup |
O(n) |
O(log(n)) |
O(1) |
Linked list
Types of Linked List
- Simple Linked List − Item navigation is forward only.
- Doubly Linked List − Items can be navigated forward and backward.
- Circular Linked List − Last item contains link of the first element as next and the first element has a link to the last element as previous.
Hash tables
They’re also known as hash maps, maps, dictionaries,and associative arrays.
Python has hash tables; they’re called dictionaries.
>>> phone_book = {}
Same as phone_book = dict()
Binary Search Tree
A Binary Search Tree is a special type of Tree that can be efficiently searched. Nodes in Binary Search Trees can have at most two chil-
dren. And nodes are positioned according to their value/key. Children nodes to the left of the parent must be smaller than the parent, children nodes to the right must be greater.
Tree Balancing
If we insert too many nodes in a Binary Search Tree, we end up with a tree of very high height, where many nodes have only one child. But we can rearrange nodes in a tree such that its height is reduced. This is called tree balancing . A perfectly balanced tree has the minimum possible height.
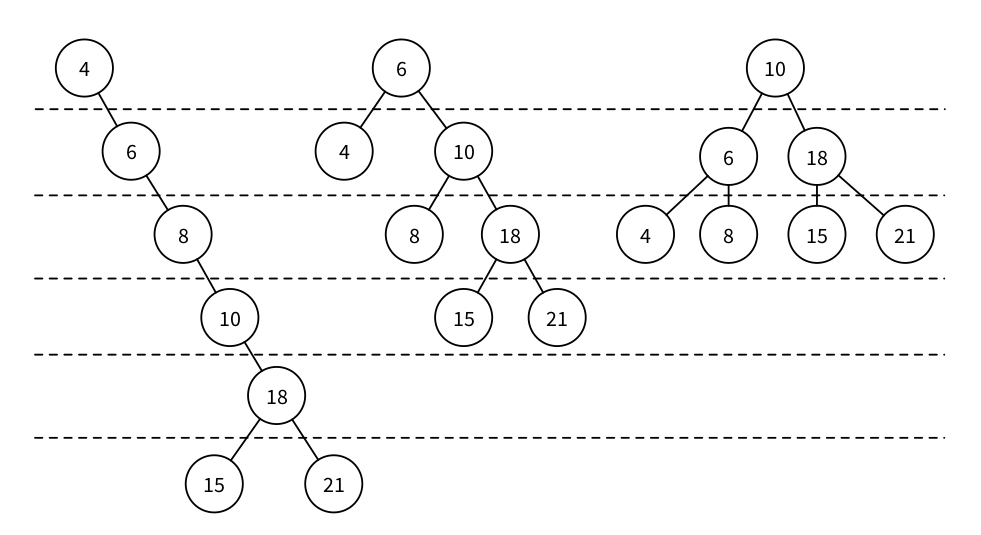
The Red-Black Tree
The Red-Black Tree is a famous example of a self-balancing tree,
which colors nodes either “red” or “black” for its balancing strat-
egy.
The AVL Tree
The AVL Tree is another breed of self-balancing trees. They
require a bit more time to insert and delete items than Red-Black
Trees, but tend to have better balancing. This means they’re faster
than Red-Black Trees for retrieving items. AVL Trees are often used
to optimize performance in read-intensive scenarios.
The Binary Heap
The Binary Heap is a special type of Binary Search Tree, in which
we can find the smallest (or highest) item instantly. This data structure is especially useful for implementing Priority Queues. In the Heap it costs O(1) to get the minimum (or maximum) item, be-
cause it is always the Root Node of the tree. Searching or inserting
nodes still costs O( log n) . It has the same node placement rules
as the Binary Search Tree, plus an extra restriction: a parent node
must be greater (or smaller) than both its child nodes.

The Graph
The Graph is similar to the Tree. The difference is that there’s no
children or parent nodes, and therefore, no Root Node.
For example, graphs are ideal for representing a social network, where nodes are people and edges represent friendships.
Types of Graphs
- Undirected Graph - A undirected graph contains edges but the edges are not directed ones.
- Directed Graph - In a directed graph, each edge has a direction.
- Weighted Graphs - edges has weight to represent an value
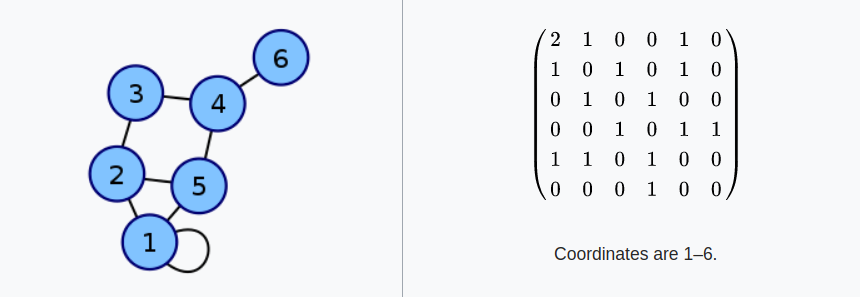
Rerpresenting Graphs
an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.
Tree
A tree in an undirectect graph with no cycles.
Breadth-first search
The algorithm to solve a shortest-path problem is called breadth-first search.
Each graph is made up of nodes and edges.
(A) —edge—> (B)
A and B are neighbors
• Question type 1: Is there a path from node A to node B?
• Question type 2: What is the shortest path from node A to node B?
Graphs
Graph Implementations
Edge lists
| One simple way to represent a graph is just a list, or array, of |
E |
∣E∣vertical bar, E, vertical bar edges, which we call an edge list. To represent an edge, we just have an array of two vertex numbers, or an array of objects containing the vertex numbers of the vertices that the edges are incident on |
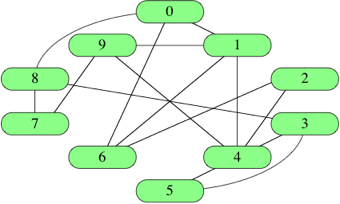
[ [0,1], [0,6], [0,8], [1,4], [1,6], [1,9], [2,4], [2,6], [3,4], [3,5],
[3,8], [4,5], [4,9], [7,8], [7,9] ]
Adjacency Matrix
| For a graph with |
V |
∣V∣vertical bar, V, vertical bar vertices, an adjacency matrix is a |
V |
\times |
V |
∣V∣×∣V∣vertical bar, V, vertical bar, times, vertical bar, V, vertical bar matrix of 0s and 1s, where the entry in row i ii and column j jj is 1 if and only if the edge (i,j) (i,j)left parenthesis, i, comma, j, right parenthesis is in the graph. |

Directed Graph
Unweighted graph boolean
Weighted graph values
Adjacency List
| Representing a graph with adjacency lists combines adjacency matrices with edge lists. For each vertex i ii, store an array of the vertices adjacent to it. We typically have an array of |
V |
∣V∣vertical bar, V, vertical bar adjacency lists, one adjacency list per vertex. |
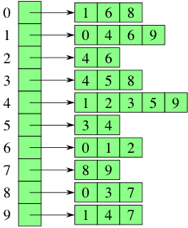
In JavaScript, we represent these adjacency lists by:
[ [1, 6, 8],
[0, 4, 6, 9],
[4, 6],
[4, 5, 8],
[1, 2, 3, 5, 9],
[3, 4],
[0, 1, 2],
[8, 9],
[0, 3, 7],
[1, 4, 7] ]
Graph Traversals
Depth First Search (DFS)
Depth First Search (DFS) algorithm traverses a graph in a depthward motion and uses a stack to remember to get the next vertex to start a search, when a dead end occurs in any iteration.
Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Push it in a stack.
Rule 2 − If no adjacent vertex is found, pop up a vertex from the stack. (It will pop up all the vertices from the
, which do not have adjacent vertices.)
Rule 3 − Repeat Rule 1 and Rule 2 until the stack is empty.
Breadth First Search (BFS)
Breadth First Search (BFS) algorithm traverses a graph in a breadthward motion and uses a queue to remember to get the next vertex to start a search, when a dead end occurs in any iteration.
Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Insert it in a queue.
Rule 2 − If no adjacent vertex is found, remove the first vertex from the queue.
Rule 3 − Repeat Rule 1 and Rule 2 until the queue is empty.
Dijkstra’s algorithm
Tree
Tree represents the nodes connected by edges.
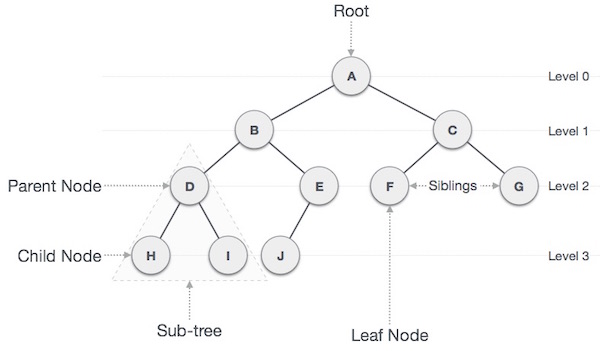
every tree have n nodes n-1 edges
Binary Search Tree
A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties −
The left sub-tree of a node has a key less than or equal to its parent node’s key.
The right sub-tree of a node has a key greater than to its parent node’s key.
https://www.youtube.com/playlist?list=PLDV1Zeh2NRsDGO4–qE8yH72HFL1Km93P
References




 Recognizes 10
also 01,001,0001,..0+1
Recognizes 10
also 01,001,0001,..0+1

















