Algorithms

26 Mar 2018

Algorithms put the science in computer science.

Permutation

If we have n items, we can order them in n factorial ( n! ) different ways.

Permutation with Identical items

The factorial n! overcounts the number of ways to order n items if some are identical. Identical items swapping their positions shouldn’t count as a different permutation.

In a sequence of n items of which r are identical, there are r! ways to reorder identical items. Thus, n! counts each distinct per- mutation r! times. To get the number of distinct permutations, we need to divide n! by this overcount factor.

For instance, the number of distinct permutations of the letters “ CODE ENERGY ” is 10!/3!

Combinations

Picture a deck of 13 cards containing all spades. How many ways can you deal six cards to your opponent? We’ve seen 13!/(13 − 6)! is the number of permutations of six out of 13 possible items. Since the order of the six cards doesn’t matter, we must divide this by 6! to obtain:

13!/6!(13-60)!

a permutation is an ordered combination

Sum

Calculating sums of sequences occurs often when counting. Sequen- tial sums are expressed using the capital-sigma ( Σ ) notation.

4
∑ (2i + 1) = 1 + 3 + 5 + 7 + 9.
i=0

Example 1

You need to fly to New York City anytime in the next 30 days.
Air ticket prices change unpredictably according to the departure 
and  return dates.How many pairs of days must be checked to find 
the cheapest tickets for flying to NYC and back within the next 30 days?

Solution

Hence, 30 pairs begin with day 1, 29 pairs begin with
day 2, 28 with day 3, and so on. 
There’s only one pair that begins on day 30.
So 30+29+...+2+1 is the total number of pairs ∑ 30

30
∑ i = 30(30 + 1)/2 = 465 pairs
i=1

Example 2

1,2,3,4,5
how many 3 digit odd numbers can be formed?

Solution

4way x 3way x 1 = 12
4way x 3way x 3 = 12
4way x 3way x 5 = 12

sum 36 ways

Strategy

Handle repetitive tasks through iteration , Iterate elegantly using recursion , Use brute force when you’re lazy but powerful, Test bad options and then backtrack , Save time with heuristics for a reasonable way out, Divide and conquer your toughest opponents, Identify old issues dynamically not to waste energy again, Bound your problem so the solution doesn’t escape.

The iterative strategy consists in using loops (e.g. for , while ) to repeat a process until a condition is met. Each step in a loop is called an iteration .

the power set (or powerset) of any set S is the set of all subsets of S, including the empty set and S itself,

Brute Force

The brute force strategy solves problems by inspecting all of the problem’s possible solution candidates.

Backtracking

sudoku solve method

Heuristics

A heuristic method , or simply a heuristic , is a method that leads to a solution without guaranteeing it is the best or optimal one. Heuristics can help when methods like brute force or backtracking are too slow.

Greedy Algorithms

Greedy algorithms try to find a localized optimum solution, which may eventually lead to globally optimized solutions. However, generally greedy algorithms do not provide globally optimized solutions.

Alt text

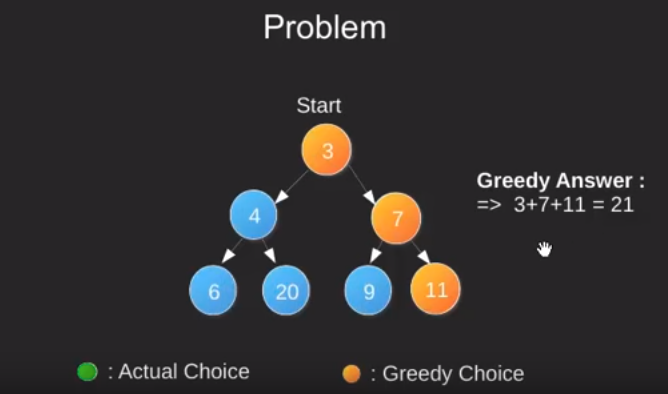
Most networking algorithms use the greedy approach. Here is a list of few of them

Travelling Salesman Problem
Prim’s Minimal Spanning Tree Algorithm
Kruskal’s Minimal Spanning Tree Algorithm
Dijkstra’s Minimal Spanning Tree Algorithm
Graph - Map Coloring
Graph - Vertex Cover
Knapsack Problem
Job Scheduling Problem

Divide and Conquer (D&C)

To recap, here’s how D&C works:

Figure out a simple case as the base case.
Figure out how to reduce your problem and get to the base case.

Example:

Suppose you’re a farmer with a plot of land. 1680x640 meters
You want to divide this farm evenly into square plots. 
You want the plots to be as big as possible. 

Figure out the base case. This should be the simplest possible case. When the recursive function will end to call itself.
Divide or decrease your problem until it becomes the base case.

Suppose one side is 25 meters (m) and the other side is 50 m. Then the largest box you can use is 25 m × 25 m. You need two of those boxes to divide up the land.

Now you need to figure out the recursive case. This is where D&C comes in. According to D&C, with every recursive call, you have to reduce your problem. How do you reduce the problem here? Let’s start by marking out the biggest boxes you can use.

So you started out with a 1680 × 640 farm that needed to be split up. But now you need to split up a smaller segment, 640 × 400. If you find the biggest box that will work for this size, that will be the biggest box that will work for the entire farm. You just reduced the problem from a 1680 × 640 farm to a 640 × 400 farm

Alt text

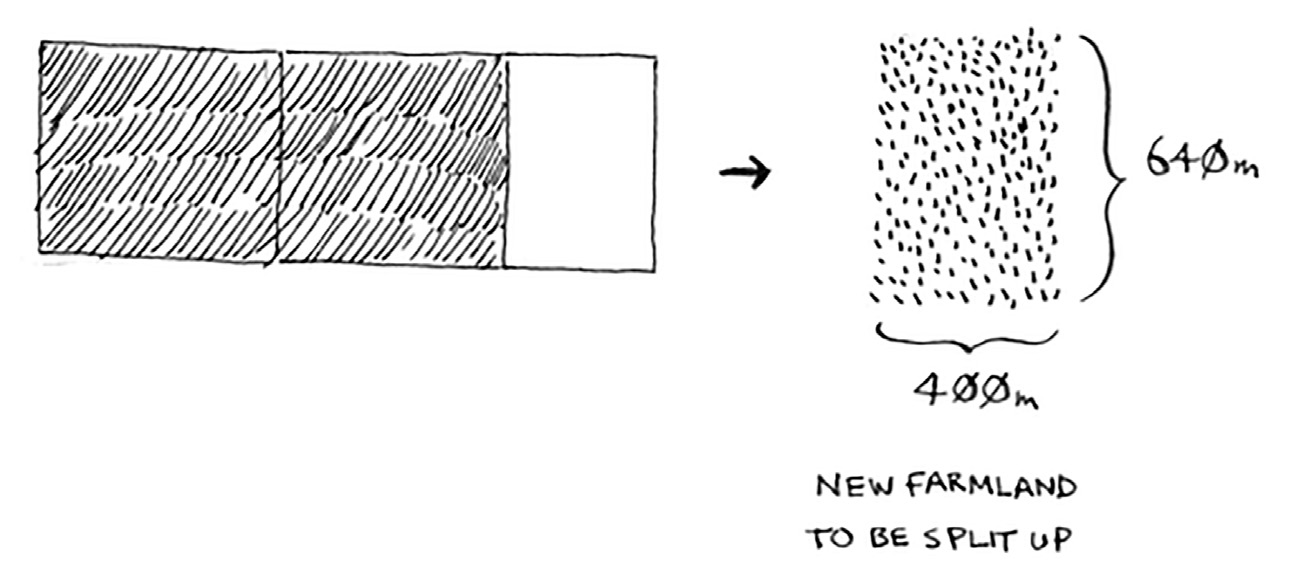
you draw a box on that to get an even smaller segment. at the end the biggest plot size you can use is 80 × 80 m

This is Euclid’s algorithm

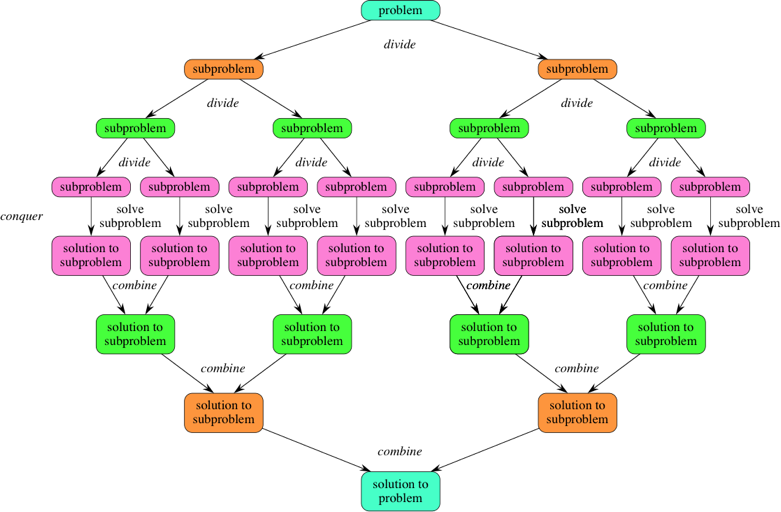
Divide the problem into a number of subproblems that are smaller instances of the same problem.
Conquer the subproblems by solving them recursively. If they are small enough, solve the subproblems as base cases.
Combine the solutions to the subproblems into the solution for the original problem.

Alt text

Dynamic Programming

Dynamic programming starts by solving subproblems and builds up to solving the big problem. Dynamic programming approach is similar to divide and conquer in breaking down the problem into smaller and yet smaller possible sub-problems.

Dynamic programming is used where we have problems, which can be divided into similar sub-problems, so that their results can be reused. Mostly, these algorithms are used for optimization. Before solving the inhand subproblem, dynamic algorithm will try to examine the results of the previously solved subproblems. The solutions of subproblems are combined in order to achieve the best solution.

It can be hard to come up with a dynamic-programming solution. That’s what we’ll focus on in this section. Some general tips follow:

Every dynamic-programming solution involves a grid.
The values in the cells are usually what you’re trying to optimize. For the knapsack problem, the values were the value of the goods.
Each cell is a subproblem, so think about how you can divide your problem into subproblems. That will help you figure out what

The following computer problems can be solved using dynamic programming approach

Fibonacci number series
Knapsack problem
Tower of Hanoi
All pair shortest path by Floyd-Warshall
Shortest path by Dijkstra
Project scheduling

Dynamic programming can be used in both top-down and bottom-up manner.

Branch and Bound

Algorithm Complexity

Analysis of algorithm is the process of analyzing the problem-solving capability of the algorithm in terms of the time and size required.

Time Factor − Time is measured by counting the number of key operations such as comparisons in the sorting algorithm.
Space Factor − Space is measured by counting the maximum memory space required by the algorithm.

Algorithm falls under three types

Best Case − Minimum time required for program execution.
Average Case − Average time required for program execution.
Worst Case − Maximum time required for program execution.
Amortized − A sequence of operations applied to the input of size a averaged over time.

BigO - how time scales with respect to some input variables

Computational Complexity

P - problems solvable in polynamial time
EXP - problems solvable in exponential time
R - problems solvable in finite time

n - input 
k - loop 

P - n , nxn
P - (n^k) 
EXP - (k^n)

NP = solvable in P on a nondeterministic machine

P ≠ NP hard to solve easy to verify(examples: riddles, puzzle without picture,secret key encryption)

O(n+c) = O(n)
O(cn) = O(n), c>0

f(n) = 7log(n)^3 + 15n^2 + 2n^3 + 8
O(f(n)) = O(n^3)

Common Asymptotic Notations

n size of the input

Constant:	O(1)
Logarithmic:	O(log(n))
Linear:		O(n)
Linearithmic:	O(nlog(n))
Quadtic:	O(n^2)
Cubic:		O(n^3)
Polynomial:	nΟ(1)
Exponential:	O(b^n)b>1
Factorial:	O(n!)

Constant Time

O(1)

a = 1
b = 2
c = a+5*b

i = 0
while i < 11
	i = i+1;

Linear Time

O(n)

i = 0
while i < n 
	i = i+1

// f(n) = n
// O((f(n))) = O(n)	

i=0
while i<n 
	i=i+3
// f(n) = n/3
// O((f(n))) = O(n)

Quadtic Time

O(n^2)

for(i = 0, i < n , i++) {
	for(j=0;j<n;j++) { // }
}

// f(n) = n*n = n^2
// O(f(n)) = O(n^2)

for(i=0;i<n;i++)
	for(j=i;j < n;j++)

Divide and Conquer (D&C)

To recap, here’s how D&C works:

Figure out a simple case as the base case.
Figure out how to reduce your problem and get to the base case.

Example:

Suppose you’re a farmer with a plot of land. 1680x640 meters

You want to divide this farm evenly into square plots. You want the plots to be as big as possible.

Figure out the base case. This should be the simplest possible case. When the recursive function will end to call itself.
Divide or decrease your problem until it becomes the base case.

Suppose one side is 25 meters (m) and the other side is 50 m. Then the largest box you can use is 25 m × 25 m. You need two of those boxes to divide up the land.

Euclid’s algorithm

Sneak peak at functional programming

Inductive proofs

Divide the problem into a number of subproblems that are smaller instances of the same problem.
Conquer the subproblems by solving them recursively. If they are small enough, solve the subproblems as base cases.
Combine the solutions to the subproblems into the solution for the original problem.

Alt text

Divide-and-conquer

The following computer algorithms are based on divide-and-conquer programming approach −

Merge Sort Quick Sort Binary Search Strassen’s Matrix Multiplication Closest pair (points)

Average case vs. worst case

Categories of algorithms

Search − Algorithm to search an item in a data structure. Sort − Algorithm to sort items in a certain order. Insert − Algorithm to insert item in a data structure. Update − Algorithm to update an existing item in a data structure. Delete − Algorithm to delete an existing item from a data structure.

Algorithm Complexity

Time Factor − Time is measured by counting the number of key operations such as comparisons in the sorting algorithm. Space Factor − Space is measured by counting the maximum memory space required by the algorithm.

Algorithm falls under three types

Best Case − Minimum time required for program execution. Average Case − Average time required for program execution. Worst Case − Maximum time required for program execution.

Common Asymptotic Notations

constant − Ο(1) logarithmic − Ο(log n) linear − Ο(n) n log n − Ο(n log n) quadratic − Ο(n2) cubic − Ο(n3) polynomial − nΟ(1) exponential − 2Ο(n)

Greedy Algorithms

Alt text

Most networking algorithms use the greedy approach. Here is a list of few of them −

Travelling Salesman Problem Prim’s Minimal Spanning Tree Algorithm Kruskal’s Minimal Spanning Tree Algorithm Dijkstra’s Minimal Spanning Tree Algorithm Graph - Map Coloring Graph - Vertex Cover Knapsack Problem Job Scheduling Problem

The Knapsack problem

The set-covering problem

Combinatorics

Approximation algorithms

Dynamic Programming

Dynamic programming starts by solving subproblems and builds up to solving the big problem.

• Dynamic programming is useful when you’re trying to optimize something given a constraint. In the knapsack problem, you had to maximize the value of the goods you stole, constrained by the size of the knapsack. • You can use dynamic programming when the problem can be broken into discrete subproblems, and they don’t depend on each other.

It can be hard to come up with a dynamic-programming solution. That’s what we’ll focus on in this section. Some general tips follow:

• Every dynamic-programming solution involves a grid. • The values in the cells are usually what you’re trying to optimize. For the knapsack problem, the values were the value of the goods. • Each cell is a subproblem, so think about how you can divide your problem into subproblems. That will help you figure out what the axes are.

The Feynman algorithm

Longest common subsequence

Longest common substring

Levenshtein distance

k-nearest neighbors

Pythagorean formula

Cosine similarity

• KNN is used for classification and regression and involves looking at the k-nearest neighbors. • Classification = categorization into a group. • Regression = predicting a response (like a number).

Dynamic Programming

Dynamic programming approach is similar to divide and conquer in breaking down the problem into smaller and yet smaller possible sub-problems.

Dynamic programming is used where we have problems, which can be divided into similar sub-problems, so that their results can be re-used. Mostly, these algorithms are used for optimization. Before solving the in-hand sub-problem, dynamic algorithm will try to examine the results of the previously solved sub-problems. The solutions of sub-problems are combined in order to achieve the best solution.

The following computer problems can be solved using dynamic programming approach −

Fibonacci number series Knapsack problem Tower of Hanoi All pair shortest path by Floyd-Warshall Shortest path by Dijkstra Project scheduling

Dynamic programming can be used in both top-down and bottom-up manner.

Sorting and Searching Algorithms

25 Mar 2018

Sorting algorithms

Classification 1. Time complexity 2. Space Complexity or Memory usage * Inplace, Constant memory * Memory usage grow with input size 3. Stability 4. Internal Sort vs External sort internal sort all records ram external sort recorts are on disk 5. Recurive or non-recursive

Selection sort

The smallest element is selected from the unsorted array and swapped with the leftmost element, and that element becomes a part of the sorted array. This process continues moving unsorted array boundary by one element to the right.

average and worst case complexities are of Ο(n2), where n is the number of items.

Selection sort

Example: Suppose you have a bunch of music on your computer. For each artist, you have a play count.

One way is to go through the list and find the most-played artist. Add that artist to a new list.

Keep doing this, and you’ll end up with a sorted list.

You check n elements, then n – 1, n - 2 … 2, 1. On average, you check a list that has 1 / 2 × n elements. The runtime is O(n × 1 / 2 × n). But constants like 1 / 2 are ignored in Big O notation (again, see chapter 4 for the full discussion), so you just write O(n × n) or O(n 2 ). This takes O(n×n) time or O(n^2) time.

very recursive function has two parts: the base case, and the recursive case. The recursive case is when the function calls itself. The base case is when the function doesn’t call itself again … so it doesn’t go into an infinite loop.

Bubble sort

This sorting algorithm is comparison-based algorithm in which each pair of adjacent elements is compared and the elements are swapped if they are not in order. This algorithm is not suitable for large data sets as its average and worst case complex

average and worst case complexity are of Ο(n2) where n is the number of items.

Insertion Sort

The array is searched sequentially and unsorted items are moved and inserted into the sorted sub-list (in the same array)

average and worst case complexity are of Ο(n2), where n is the number of items.

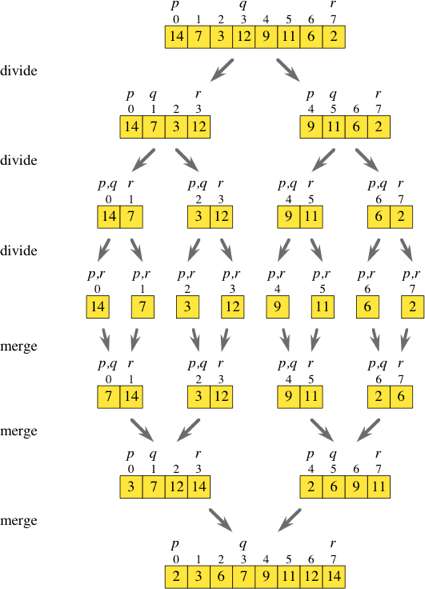
Merge sort

Merge sort is a sorting technique based on divide and conquer technique. With worst-case time complexity being Ο(n log n), it is one of the most respected algorithms.

Merge sort first divides the array into equal halves and then combines them in a sorted manner.

Divide array to arrays and achieve atomic value which can no more be divided. Now, we combine them in exactly the same manner as they were broken down

Quicksort sort

in-place memory

average-case time complexity O(nlogn) worst case time complexity O(n^2)

Binary search

With binary search, you guess the middle number and eliminate half the remaining numbers every time

Example

The dictionary has 240,000 words. Simple search could take 240,000 steps

Binary search you cut the number of words in half until you’re left with only one word. So binary search will take 18 steps

Simple search will take n steps. Binary search will take log2n steps to run in the worst case.

Binary search only works when your list is in sorted order

log10 100 is like asking, “How many 10s do we multiply together to get 100?” The answer is 2: 10 × 10.

Logs are the flip of exponentials.

If this is a list of 100 numbers, it takes up to 100 guesses. If it’s a list of 4 billion numbers, it takes up to 4 billion guesses. So the maximum number of guesses is the same as the size of the list. This is called linear time.

Binary search is different. If the list is 100 items long, it takes at most 7 guesses. If the list is 4 billion items, it takes at most 32 guesses. Powerful, eh? Binary search runs in logarithmic tim

Simple searche - O(n) Binary search - O(logn)

Big O notation lets you compare the number of operations. It tells you how fast the algorithm grows.

Big O establishes a worst-case run time

Some common Big O run times

• O(log n), also known as log time. Example: Binary search. • O(n), also known as linear time. Example: Simple search. • O(n * log n). Example: A fast sorting algorithm, like quicksort (coming up in chapter 4). • O(n 2 ). Example: A slow sorting algorithm, like selection sort (coming up in chapter 2). • O(n!). Example: A really slow algorithm, like the traveling salesperson (coming up next!).

Suppose you’re drawing a grid of 16 boxes again, and you can choose from 5 different algorithms to do so. If you use the first algorithm, it will take you O(log n) time to draw the grid. You can do 10 operations per second. With O(log n) time, it will take you 4 operations to draw a grid of 16 boxes (log 16 is 4). So it will take you 0.4 seconds to draw the grid. What if you have to draw 1,024 boxes? It will take you log 1,024 = 10 operations, or 1 second to draw a grid of 1,024 boxes. These numbers are using the first algorithm.

• Algorithm speed isn’t measured in seconds, but in growth of the number of operations. • Instead, we talk about how quickly the run time of an algorithm increases as the size of the input increases. • Run time of algorithms is expressed in Big O notation. • O(log n) is faster than O(n), but it gets a lot faster as the list of items you’re searching grows.

Array reading O(1) Array insertion O(n) Array Delete O(n) Lists reading O(n) Lists Insertion O(1) Lists Insertion O(1)

There are two different types of access: random access and sequential access.

Linked lists are good for inserts/deletes, and arrays are good for random access.

Let’s consider a hybrid data structure: an array of linked lists. You have an array with 26 slots. Each slot points to a linked list. For example, the first slot in the array points to a linked list containing all the usernames starting with a. The second slot points to a linked list containing all the usernames starting with b, and so on.

Traveling salesperson problem.

The salesperson has to go to five cities. This salesperson, whom I’ll call Opus, wants to hit all five cities while traveling the minimum distance.

5! = 120 There are 120 permutations with 5 cities,

In general, for n items, it will take n! (n factorial) operations to compute the result. So this is O(n!) time, or factorial time

Tree

Binary search tree

• B-trees • Red-black trees • Heaps • Splay trees

Inverted indexes

The Fourier transform

Parallel algorithms

MapReduce

Distributed algorithm

Interpolation Search

Hash Table

Collisions

To avoid collisions, you need • A low load factor • A good hash function

Load factor

number of items in hash table / total number of slots

2/5 = 0.4

Suppose you need to store the price of 100 produce items in your hash table, and your hash table has 100 slots. In the best case, each item will get its own slot. This hash table has a load factor of 1

Once the load factor starts to grow, you need to add more slots to your hash table. This is called resizing.

array size 4 load factor - 4/3 resize hash table array size 8 load factor - 8/3

“This resizing business takes a lot of time!” And you’re right. Resizing is expensive, and you don’t want to resize too often. But averaged out, hash tables take O(1) even with resizing.

A good hash function distributes values in the array evenly. A bad hash function groups values together and produces a lot of collisions.

Arithmetic Sets

17 Mar 2018

Set is collection of distinct objects

∅ - is null set

Membership

A = {1,2,3,4}
4 ∈ A 
9 ∉ A 

Equality

A is {1, 2, 3}
B is {3, 1, 2}

A = B

Unions

Two sets can be “added” together. The union of A and B, denoted by A ∪ B, is the set of all things that are members of either A or B.

{1, 2} ∪ {1, 2} = {1, 2}
{1, 2} ∪ {2, 3} = {1, 2, 3}
{1, 2, 3} ∪ {3, 4, 5} = {1, 2, 3, 4, 5}

Intersections

{1, 2} ∩ {1, 2} = {1, 2}
{1, 2} ∩ {2, 3} = {2}

Complements

Two sets can also be “subtracted”. The relative complement of B in A (also called the set-theoretic difference of A and B), denoted by A \ B (or A − B)

A′ = U \ A

{1, 2} \ {1, 2} = ∅.
{1, 2, 3, 4} \ {1, 3} = {2, 4}.

A \ B ≠ B \ A  for A ≠ B.

Universal set and absolute complement

U  - Universal set
A′ - All things in the universe that are not in A

A′ = U \ A = U - A

C = {0,5,15,3}

0 ∈ C 
12 ∉ C

C′ = U\C = U-C

0 ∉ C′ 
12 ∈ C′

Subsets

If every member of set A is also a member of set B, then A is said to be a subset of B, written A ⊆ B (also pronounced A is contained in B). Equivalently, we can write B ⊇ A, read as B is a superset of A, B includes A, or B contains A. The relationship between sets established by ⊆ is called inclusion or containment.

subset of this is {1, 2, 3}. Another subset is {3, 4} or even another is {1}, etc.

{1, 3} ⊆ {1, 2, 3, 4}.
{1, 2, 3, 4} ⊆ {1, 2, 3, 4}.

The empty set is a subset of every set and every set is a subset of itself:

∅ ⊆ A.
A ⊆ A.

Every set is a subset of the universal set:

A ⊆ U.

number of subset of set is 2^n
n is number of elements

Proper Subsets (strict subsets)

If A is a subset of, but not equal to, B, then A is called a proper subset of B, written A ⊊ B (A is a proper subset of B) or B ⊋ A (B is a proper superset of A).

{1, 2, 3} is a subset of {1, 2, 3}, 
but is not a proper subset of {1, 2, 3}.

{1, 2, 3} is a proper subset of {1, 2, 3, 4}
because the element 4 is not in the first set.

{1, 2, 3, 4}  is a proper superset of {1, 2, 3}

{1, 2, 3} ⊆ {1, 2, 3}
{1, 2, 3} ⊊ {1, 2, 3, 4} we can say {1, 2, 3} ⊆ {1, 2, 3, 4}
{1, 2, 3, 4} ⊋ {1, 2, 3} 

Posibile Subset

{1, 2, 3}
subsets
{} or ∅,{1},{2},{3},{1,2},{1,3},{2,3},{1, 2, 3}

References

https://en.wikipedia.org/wiki/Set_(mathematics)/

Arithmetic Series

06 Mar 2018

Arithmetic series

A series is the sum of a sequence

seq = {1,2,3,4,5,6,...,n}

sum1 = 1+2+3+4 ... n
sum2 = n + (n-1) + (n-2) + (n-3) ..   

sum1+sum2 = (n+1) + (n+1) + (n+1) + (n+1) ...

2sum = n(n+1);
sum = n(n+1)/2

n - last 
1 - first

Arithmetic sequences

A sequence is an ordered list of elements

seq = {1,5,9,13..}

f(n) = 1 + 4(n-1)

sum of seq 
d = 4
a = 1

sum1  = a + (a + d) + (a + 2d) + (a + 3d) + ... + (a + (n-1)d)
sum2  = (a + (n-1)d) + (a + (n-2)d) + (a + (n-3)d) + .. (a + (n - z)d)
sum3  = sum1 + sum2 = a + (a + (n-1)d) + (a + d) + (a + (n-2)d) .... 
sum3  = 2a + (n-1)d + 2a + (n-1)d.... = n(2a+(n-1)d)

sum = (2a+(n-1)d)/2

n( a +  a + (n-1)d) / 2 
first half a/2  + last haft (a + (n-1)d)/2 multiply n times

Example 1

11+20+29+...+4052

Solution 1

d = 9
a = 11
11 + 9(n-1) = 4052
9n = 4050
n = 450

Solution 2

(4052-11)/9=449

from 11 to reach 4052 you nead 499 steps 
add first step 450 steps

The sum of a series

sum = (2a+(n-1)d)/2

((2x11 + (550-1)x9/2) x 450

((11+4052)/2)x450

Example 2

10+(−1)+(−12)+...+(−10,979)=
10-11(n-1) = - 10979

n = 1000

((10 +(-10979))/2)x1000  = -5484500

Example 3

k=1
∑ (−5k+12)= ?
275
​	 
−5k+12=7      k=1
−5k+12=-1363  k=275

sum = ((-1363+7)/2)x275 = -186450

Geometric series

a = first term
r =  common ratio
n = # of terms
Sn = sum of n terms

Sn = a + ar + ar^2 + ... ar^n-1
-rSn = -ra - ar^2 - ... - ar^n

Sn  - rSn = a - ar^n
Sn(1-r) = a - ar^n

Sn  = (a-ar^n )/1-r 

Assembly

10 Feb 2018

Assebly

Register

To speed up the processor operations, the processor includes some internal memory storage locations, called registers.

There are ten 32-bit and six 16-bit processor registers in IA-32 architecture.

The registers are grouped into three categories −

General registers, Control registers, and Segment registers. The general registers are further divided into the following groups −

Data registers, Pointer registers, and Index registers.

Data Registers

System calls are APIs for the interface between the user space and the kernel space.

Nibbles

A nibble is a collection of four bits

Bytes

Bits 0..3 comprise the low order nibble, bits 4..7 form the high order nibble. Since a byte contains exactly two nibbles, byte values require two hexadecimal digits.

Since a byte contains eight bits, it can represent 28, or 256, different values. Generally, we’ll use a byte to represent numeric values in the range 0..255, signed numbers in the range -128..+127

Words

A word is a group of 16 bits.

Double Words

A double word is exactly what its name implies, a pair of words.

Signed and Unsigned Numbers

with n bits we can represent the signed values in the range -2n-1 to +2n-1-1.

00000000	+0	0
00000001	1	1
⋮	⋮	⋮
01111101	125	125
01111110	126	126
01111111	127	127
10000000	−127	128
10000001	−126	129
10000010	−125	130
⋮	⋮	⋮
11111101	−2	253
11111110	−1	254
11111111	−0	255

1) Invert all the bits in the number 2) Add one to the inverted result

0000 0101 Five (in binary). 1111 1010 Invert all the bits. 1111 1011 Add one to obtain result.

Shifts and Rotates

Another set of logical operations which apply to bit strings are the shift and rotate operations. These two categories can be further broken down into left shifts, left rotates, right shifts, and right rotates.

shifting it left multiplies it by two.

If you shift a binary value to the left three times, you multiply it by eight (222) If you perform n right shifts, you will divide that number by 2n

The ASCII Character Set

Von Neumann architecture (VNA)

Buses

The system bus

The system bus connects the various components of a VNA machine

The Data Bus

The Address Bus

The Control Bus

The CPU sends data to memory and receives data from memory on the data bus. This prompts the question, “Is it sending or receiving?” There are two lines on the control bus, read and write, which specify the direction of data flow

The 80x86 family deals with this problem by storing the L.O. byte of a word at the address specified and the H.O. byte at the next location

CPU Registers

AX –The accumulator register BX –The base address register CX –The count register DX –The data register

Besides the above registers, which are visible to the programmer, the x86 processors also have an instruction pointer register which contains the address of the next instruction to execute. There is also a flags register that holds the result of a comparison. The flags register remembers if one value was less than, equal to, or greater than another value.

Because registers are on-chip and handled specially by the CPU, they are much faster than memory

Accessing a memory location requires one or more clock cycles. Accessing data in a register usually takes zero clock cycles

The Arithmetic & Logical Unit

For example, if you want to add the value five to the AX register, the CPU: • Copies the value from AX into the ALU, • Sends the value five to the ALU, • Instructs the ALU to add these two values together, • Moves the result back into the AX register.

The Bus Interface Unit

The bus interface unit (BIU) is responsible for controlling the address and data busses when accessing main memory. If a cache is present on the CPU chip then the BIU is also responsible for accessing data in the cache.

The Control Unit and Instruction Sets

CBA Instruction 000 move 001 add 010 subtract 011 multiply 100 divide 101 and 110 or 111 xor DD SS DD -or- SS Register 00 AX 01 BX 10 CX 11 DX

log2(n)

The move instruction would move data from the source register to the destination register the add instruction would add the value of the source register to the destination register, etc.

The x86 Instruction Set

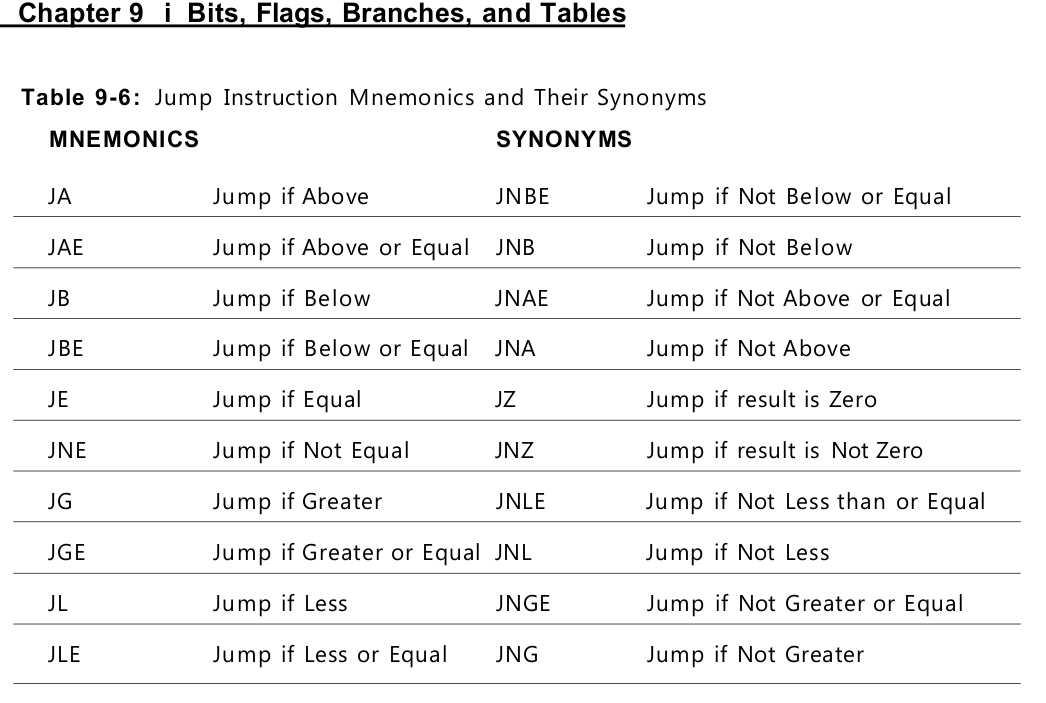
The instructions are mov (two forms), add, sub, cmp, and, or, not, je, jne, jb, jbe, ja, jae, jmp, brk, iret, halt, get, and put.

mov reg, reg/memory/constant mov memory, reg

The arithmetic and logical instructions

add reg, reg/memory/constant
sub reg, reg/memory/constant
cmp reg, reg/memory/constant
and reg, reg/memory/constant
or reg, reg/memory/constant
not reg/memory

The add instruction adds the value of the second operand to the first (register) operand, leaving the sum in the first operand. The sub instruction subtracts the value of the second operand from the first, leaving the difference in the first operand. The cmp instruction compares the first operand against the second and saves the result of this comparison for use with one of the conditional jump instructions (described in a moment). The and and or instructions compute the corresponding bitwise logical operation on the two operands and store the result into the first operand. The not instruction inverts the bits in the single memory or register operand.

The control transfer instructions

ja dest – Jump if above jae dest – Jump if above or equal jb dest – Jump if below jbe dest – Jump if below or equal je dest – Jump if equal jne dest – Jump if not equal jmp dest – Unconditional jump iret – Return from an interrupt

The first six instructions in this class let you check the result of the previous cmp instruction for greater than, greater or equal, less than, less or equal, equality, or inequality

Addressing Modes on the x86

The x86 processors support the register addressing mode10, the immediate addressing mode, the indirect addressing mode, the indexed addressing mode, and the direct addressing mode.

mov ax, [1000] mov ax, [bx] mov ax, [1000+bx]

The first instruction above uses the direct addressing mode to load ax with the 16 bit value stored in memory starting at location 1000 hex. The mov ax, [bx] instruction loads ax from the memory location specified by the contents of the bx register. This is an indirect addressing mode

mov bx, 1000 mov ax, [bx]

are equivalent to the single instruction:

mov ax, [1000]

Of course, the second sequence is preferable

The last memory addressing mode is the indexed addressing mode. An example of this memory addressing mode is mov ax, [1000+bx]

3.3.7 Encoding x86 Instructions

i i i r r m m m
i i i
= special
= or
= and
= cmp
= sub
= add
= mov reg, mem/reg/const
= mov mem, reg

r r
= AX
= BX
= CX
= DX

mmm
0 0 = AX
0 1 = BX
1 0 = CX
1 1 = DX
0 0 = [BX]
0 1 = [xxxx+BX]
1 0 = [xxxx]
1 1 = constant

0 0 i i m m m

i i
= zero operand instructions
= jump instructions
= not
= illegal (reserved)

mmm (if ii = 10)
= AX
= BX
= CX
= DX
= [BX]
= [ xxxx+BX]
= [ xxxx]
= constant

For example, to encode the mov ax, bx instruction you would select iii=110 (mov reg, reg), rr=00 (ax), and mmm=001 (bx). This produces the one-byte instruction 11000001 or 0C0h.

0 0 0 0 i i i
i i i
= illegal
= illegal
= illegal
= brk
= iret
= halt
= get
= put

0 0 0 1 i i i
mmm (if ii = 10)
= j e
= jne
= j b
= jbe
= j a
= jae
= jmp
= illegal

jxx address The jmp instruction copies the 16-bit immediate value (address) following the opcode into the IP register. Therefore, the CPU will fetch the next instruction from this target address; effectively, the program “jumps” from the point of the jmp instruction to the instruction at the target address.

Three of these instructions are illegal instruction opcodes. The brk (break) instruction pauses the CPU until the user manually restarts it. This is useful for pausing a program during execution to observe results. The iret (interrupt return) instruction returns control from an interrupt service routine. We will discuss interrupt service routines later. The halt program terminates program execution. The get instruction reads a hexadecimal value from the user and returns this value in the ax register; the put instruction outputs the value in the ax register.

Step-by-Step Instruction Execution

the mov reg, reg/memory/constant instruction: • Fetch the instruction byte from memory. • Update the ip register to point at the next byte. • Decode the instruction to see what it does. • If required, fetch a 16-bit instruction operand from memory. • If required, update ip to point beyond the operand. • Compute the address of the operand, if required (i.e., bx+xxxx) . • Fetch the operand. • Store the fetched value into the destination register

section.data text db “Hello, World!”, 10

section .text global _start _start: mov rax, 1 mov rdi, 1 mov rsi, text mov rdx, 14 syscall

mov rax, 60
mov rdi, 0
syscall

text db “Hello, World!”, 10

db define bite 10 is new line \n

text name of memmory address

• A bit is a single binary digit, 0 or 1. • A byte is 8 bits side by side. • A word is 2 bytes side by side. • A double word is 2 words side by side. • A quad word is 2 double words side by side.

The Linux kernel was entirely separate from the user interface, and it was protected from damage due to malfunctioning programs elsewhere in the system. System memory was tagged as either kernel space or user space, and nothing running in user space could write to (nor generally read from) anything stored in kernel space. Communication between kernel space and user space was handled through strictly controlled system calls

Direct access to physical hardware, including memory, video, and periph- erals, was limited to software running in kernel space. Programs wishing to make use of system peripherals could only get access through kernel-mode device drivers.

Memory model

The oldest and now ancient memory model is called the real mode flat model

The newest memory model is called protected mode flat model, and it’s the memory model behind modern operating systems such as Windows 2000/XP/Vista/7 and Linux.

Real mode flat model is very much like protected mode flat model in miniature.

NAME VALUE IN DECIMAL VALUE IN HEX Byte 1 01H Word 2 02H Double word 4 04 H Quad word 8 08H Ten byte 10 OAH Paragraph 16 10H Page 256 100H Segment 65,536 10000H

The segment registers exist only to hold segment addresses.

The segment registers have names that reflect their general functions: CS, DS, SS, ES, FS, and GS. FS and GS exist only in the 386 and later Intel x86 CPUs—but are still 16 bits in size. All segment registers are 16 bits in size, irrespective of the CPU. This is true even of the 32-bit CPUs.

• CS stands for code segment. Machine instructions exist at some offset into a code segment. The segment address of the code segment of the currently executing instruction is contained in CS. DS stands for data segment. Variables and other data exist at some offset into a data segment. There may be many data segments, but the CPU may only use one at a time, by placing the segment address of that segment in register DS. SS stands for stack segment. The stack is a very important component of the CPU used for temporary storage of data and addresses. I explain how the stack works a little later; for now simply understand that, like everything else within real mode’s megabyte of memory, the stack has a segment address, which is contained in SS. ES stands for extra segment. The extra segment is exactly that: a spare segment that may be used for specifying a location in memory. FS and GS are clones of ES. They are both additional segments with no specific job or specialty. Their names come from the fact that they were created after ES (think, E, F, G). Don’t forget that they exist only in the 386 and later x86 CPUs!

these general-purpose registers are used to hold the offset addresses that must be paired with segment addresses to pin down a single location in memory.

The ‘‘bitness’’ of the world is almost entirely defined by the width of the x86 CPU registers.

Adding a room to your house doesn’t make it two houses—just one bigger house.

There are eight 16-bit general-purpose registers: AX, BX, CX, DX, BP, SI, DI, and SP. They are all 16 bits in size, and you can place any value in them that may be expressed in 16 bits or fewer.

When Intel expanded the x86 architecture to 32 bits in 1986, it doubled the size of all eight registers and gave them new names by prefixing an E in front of each register name, resulting in EAX, EBX, ECX, EDX, EBP, ESI, EDI, and ESP.

EAX, EBX, ECX, and EDX, but there’s an additional twist: the low 16 bits are themselves divided into two 8-bit halves, so what we have are register names on not two but three levels

The 16-bit registers AX, BX, CX, and DX are present as the lower 16-bit portions of EAX, EBX, ECX, and EDX; but AX, BX, CX, and DX are themselves divided into 8-bit halves, and assemblers recognize special names for the two halves. The A, B, C, and D are retained, but instead of the X, a half is specified with an H (for high half) or an L (for low half). Each register half is one byte (8 bits) in size.

BX there is BH and BL

The Instruction Pointers

usually called IP or, in 32-bit protected mode, EIP

It can do only one thing: it contains the offset address of the next machine instruction to be executed in the current code segment.

A code segment is an area of memory where machine instructions are stored.

The current code segment is that code segment whose segment address is currently stored in code segment register CS.

Together, CS and IP contain the full address of the next machine instruction to be executed.

The nature of this address depends on what CPU you’re using, and the programming model for which you’re using it

The Flags Register

The Three Major Assembly Programming Models

Real Mode Flat Model

CS always points to the current code segment, and the next instruction to be executed is pointed to by the IP register

You can destroy portions of the operating system by careless use of segment registers, which will cause the operating system to crash and take your program with it. This is the danger that prompted Intel to build new features into its 80386 and later CPUs to support a ‘‘protected’’ mode. In protected mode, application programs (that is, the programs that you write, as opposed to the operating system or device drivers) cannot destroy the operating system or other application programs that happen to be running elsewhere in memory via multitasking. That’s what the protected means.

The 64-bit versions of the registers are renamed beginning with an R: EAX becomes RAX, EBX becomes RBX, and so on.

Linux comes with its own linker, called ld.

Everything is a file.

When you read from a file, you are accepting data from an endpoint. The path that the data takes between files may be entirely within a single computer, or it may be between computers along a network of some kind. Data may be processed and changed along the path, or it may simply move from one endpoint to another without modification. No matter. Everything is a file, and all files are treated more or less identically by Unix’s internal file machinery

Your keyboard is a file: it’s an endpoint that generates data and sends it somewhere. Your display is a file: it’s an endpoint that receives data from somewhere and puts it where you can see it. Unix files do not have to be text files. Binary files (like the executables created by NASM and the linker) are handled the same way.

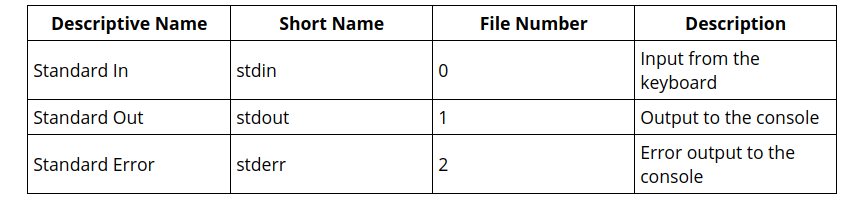
				FILE C IDENTIFIER	FILE DESCRIPTOR 	DEFAULTS TO Standard Input 		stdin 				0 					Keyboard Standard Output 	stdout 				1 					Display Standard Error 		stderr 				2  					Display

but it’s good to know that the power is there as your programming skills improve and you take on more ambitious projects.

By convention in assembly language, the first (leftmost) operand belonging to a machine instruction is the destination operand. The second operand from the left is the source operand.

Three different flavors of data may be used as operands: memory data, register data, and immediate data.

you can move an immediate value to memory, or a memory value to a register, or some other similar combination, but you can’t move a memory value directly to another memory value. This is just an inherent limitation of the current generation of x86 CPUs, and we have to live with it, inconvenient as it is at times.

to move the word in memory at the address contained in EBX into register EAX, you would use the following instruction: mov eax,[ebx]

EatMsg: db “Eat at Joe’s!” mov ecx,EatMsg

If you’ve had any exposure to high-level languages like Pascal, your first instinct might be to assume that whatever data is stored in EatMsg will be copied into ECX. Assembly doesn’t work that way. That MOV instruction actually copies the address of EatMsg, not what’s stored in (actually, at) EatMsg. In assembly language, variable names represent addresses, not data!

So how do you actually ‘‘get at’’ the data represented by a variable like EatMsg? Again, it’s done with square brackets: mov edx,[EatMsg]

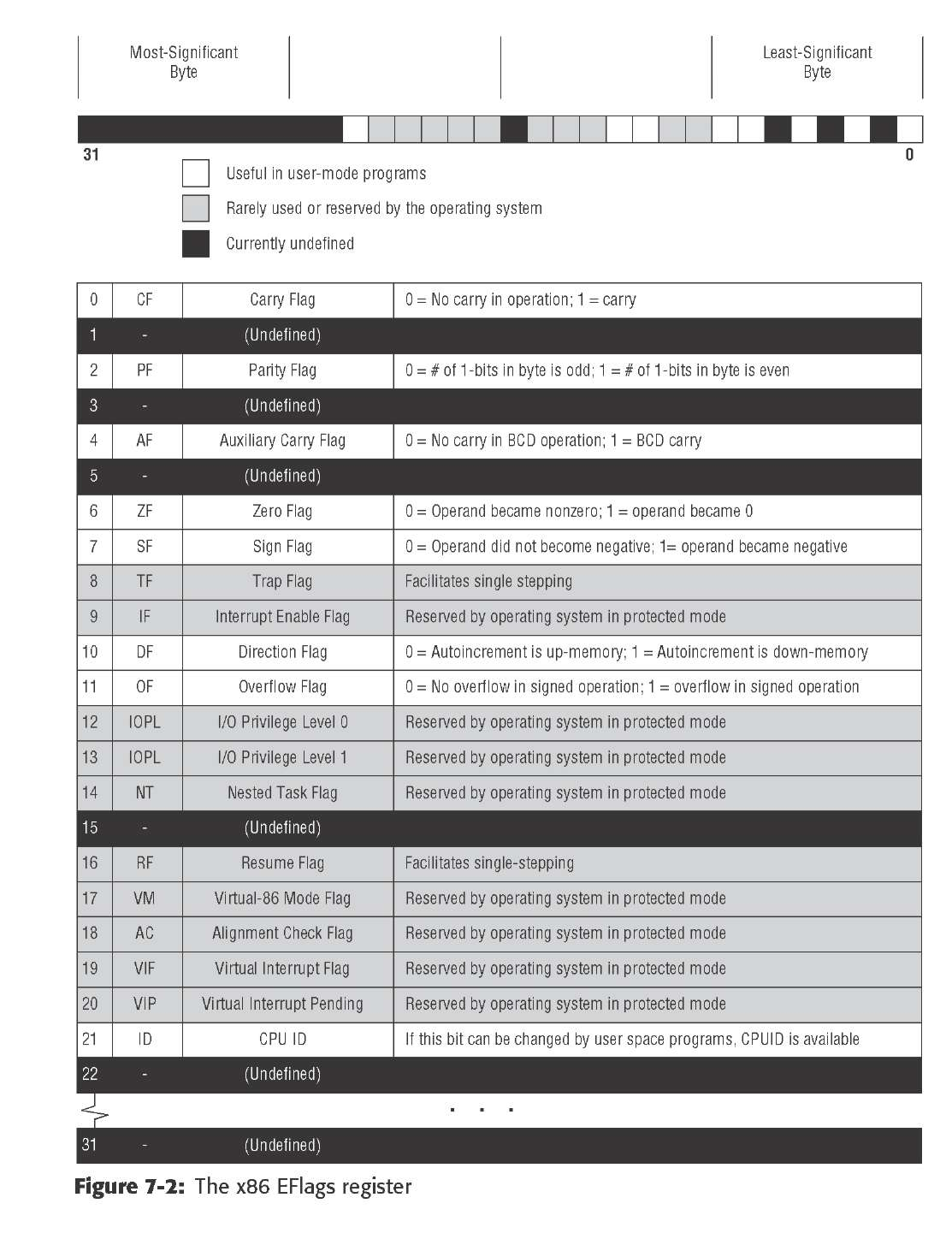
EFlags as a whole is a single 32-bit register buried inside the CPU. It’s the 32-bit extended descendent of the 16-bit Flags register present in the 8086/8088 CPUs

• OF: The Overflow flag is set when the result of an arithmetic operation on a signed integer quantity becomes too large to fit in the operand it originally occupied. OF is generally used as the ‘‘carry flag’’ in signed arithmetic.

Alt text

Several x86 machine instructions come in pairs. Simplest among those are INC and DEC,

Every executable program for Linux has to have a label _ s t a r t in it somewhere, irrespective of the language it’s written in: C, Pascal, assembly, no matter. If the Linux loader can’t find the label, it can’t load the program correctly. The g l o b a l specifier tells the linker to make the _ s t a r t label visible from outside the program’s borders.

MyByte db 07h ; 8 bits in size MyWord dw 0FFFFh ; 16 bits in size MyDouble dd 0B8000000h ; 32 bits in size

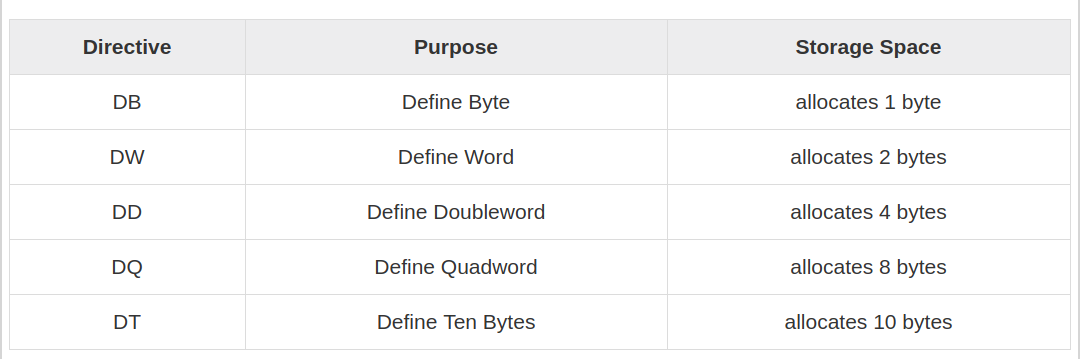
Think of the DB directive as ‘‘Define Byte.’’ DB sets aside one byte of memory for data storage. Think of the DW directive as ‘‘Define Word.’’ DW sets aside one word (16 bits, or 2 bytes) of memory for data storage. Think of the DD directive as ‘‘Define Double.’’ DD sets aside a double word in memory for storage, typically for full 32-bit memory addresses.

TwoLineMsg: db “Eat at Joe’s…“,10,”…Ten million flies can’t ALL be wrong!”,10

What’s with the numeric literal 10 tucked into the previous example strings? In Linux text work, the end-of-line (EOL) character has the numeric value of 10. It indicates to the operating system where a line submitted for display to the Linux console ends.

You can concatenate such individual numbers within a string, but you must remember that, as with EOL, they will not appear as numbers. A string is a string of characters. A number appended to a string will be interpreted by most operating system routines as an ASCII character.

You can define string variables using DW or DD, but they’re handled a little differently than those defined using DB. Consider these variables: WordString: dw CQ 1

DoubleString: dd ‘Stop’ The DW directive defines a word-length variable, and a word (16 bits) may hold two 8-bit characters. Similarly, the DD directive defines a double word (32-bit) variable, which may hold four 8-bit characters.

A statement containing the directive EQU is called an equate. An equate is a way of associating a value with a label. Such a label is then treated very much like a named constant in Pascal. Any time the assembler encounters an equate during an assembly, it will swap in the equate’s value for its name. For example:

FieldWidth equ

The preceding tells the assembler that the label F i e l d w i d t h stands for the numeric value 10. Once that equate is defined, the following two machine instructions are exactly the same:

mov eax,10 mov eax,FieldWidth

EatLen: equ $-EatMsg

The assembly-time calculation is to take the location represented by the $ token (which, when the calculation is done, contains the location just past the end of the E a t M s g string) and subtract from it location of the beginning of the E a t M s g string. End - Beginning = Length

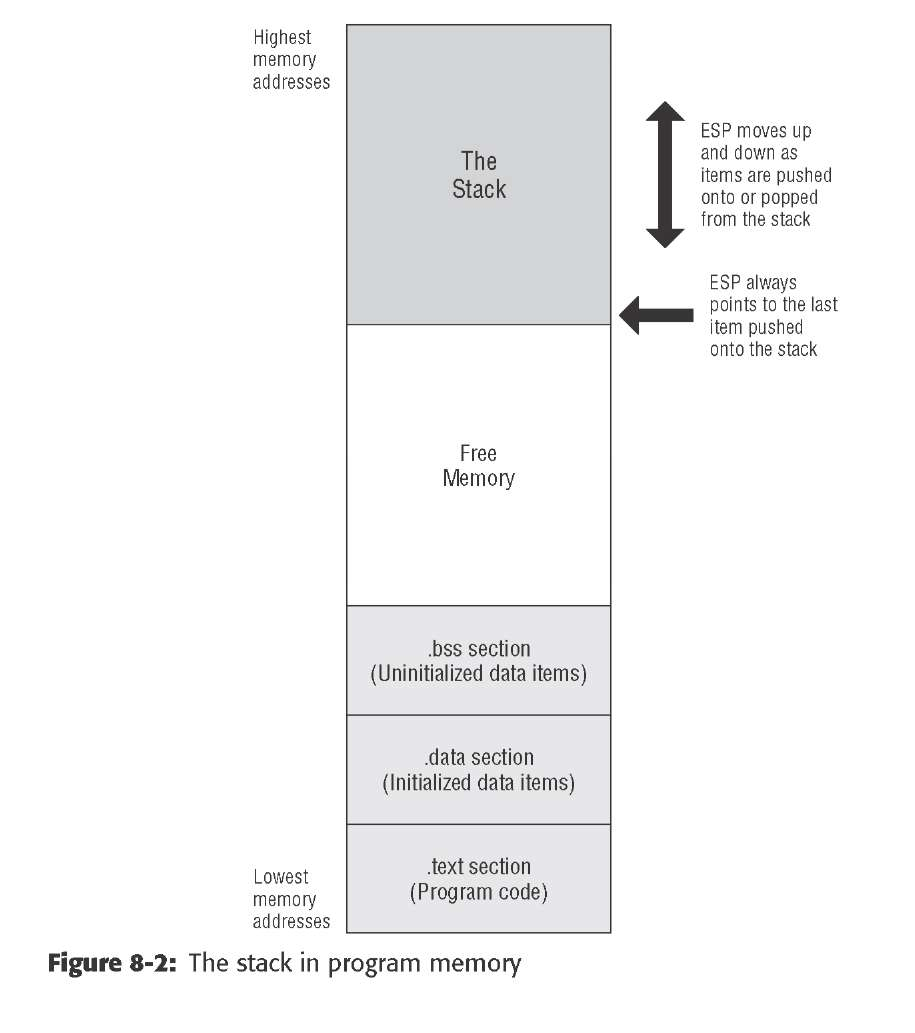
In the x86 architecture, the top of the stack is marked by a register called the stack pointer, with the formal name ESP. It’s a 32-bit register, and it holds the memory address of the last item pushed onto the stack.

the stack begins up at the ceiling, and as items are pushed onto the stack, the stack grows downward, toward low memory.

Alt text

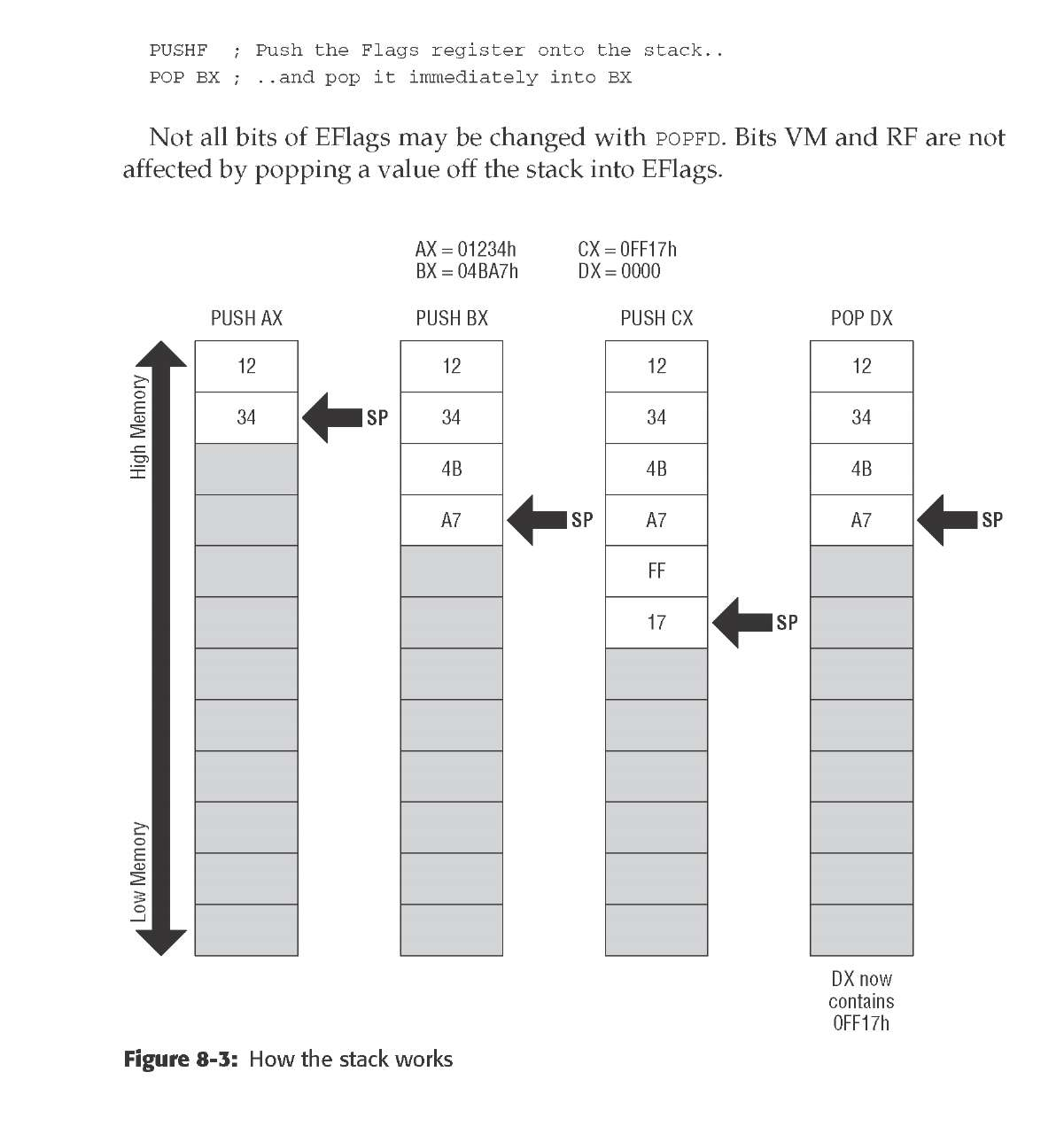
Push-y Instructions You can place data onto the stack in several ways, but the most straightforward way involves a group of five related machine instructions: PUSH, PUSHF, PUSHFD, PUSHA, and PUSHAD. All work similarly, and differ mostly in what they push onto the stack: PUSH pushes a 16-bit or 32-bit register or memory value that is specified by you in your source code.

• PUSHF pushes the 16-bit Flags register onto the stack. • PUSHFD pushes the full 32-bit EFlags register onto the stack. • PUSHA pushes all eight of the 16-bit general-purpose registers onto the stack. • PUSHAD pushes all eight of the 32-bit general-purpose registers onto the stack.

Alt text

One excellent use of the stack allows the all-too-few registers to do multiple duty. If you need a register to temporarily hold some value to be operated on by the CPU and all the registers are in use, push one of the busy registers onto the stack. Its value will remain safe on the stack while you use the register for other things. When you’re finished using the register, pop its old value off the stack—and you’ve gained the advantages of an additional register without really having one

kernel services call gate

pooling

INT 00h - 0FFh 256 interrupts

The physical address is calculated from 2 parts. i) segment address. ii) offset address. The CS(code segment register) is used to address the code segment of the memory i.e a location in the memory where the code is stored. The IP(Instruction pointer) contains the offset within the code segment of the memory. Hence CS:IP is used to point to the location (i.e to calculate the physical address)of the code in the memory.

Since IP is 16 bit it means you can only have 64k instructions (2^16), which wasn’t much even in the 80s. So to expand the address space you have a second register which addresses 64k blocks. You could consider cs:ip together as one 32 bit register which is then capable of addressing 2^32 bytes…ie 4G which is what you get on a processor which uses 32 bit addresses. The 8086 was using 20 bits of addresses, so you could access 1M of memory.

INT 00h - 0FFh 256 interrupts

Executes the INT instuction
Interprets the INT instruction during the assembly time
Moves the INT instruction to the Vector Table
1. Vector Table occupies location 00 to 3FF of the program memory
2. It contains the Code Segment(CS) and Instruction Pointer(IP) for each kind of interrupt

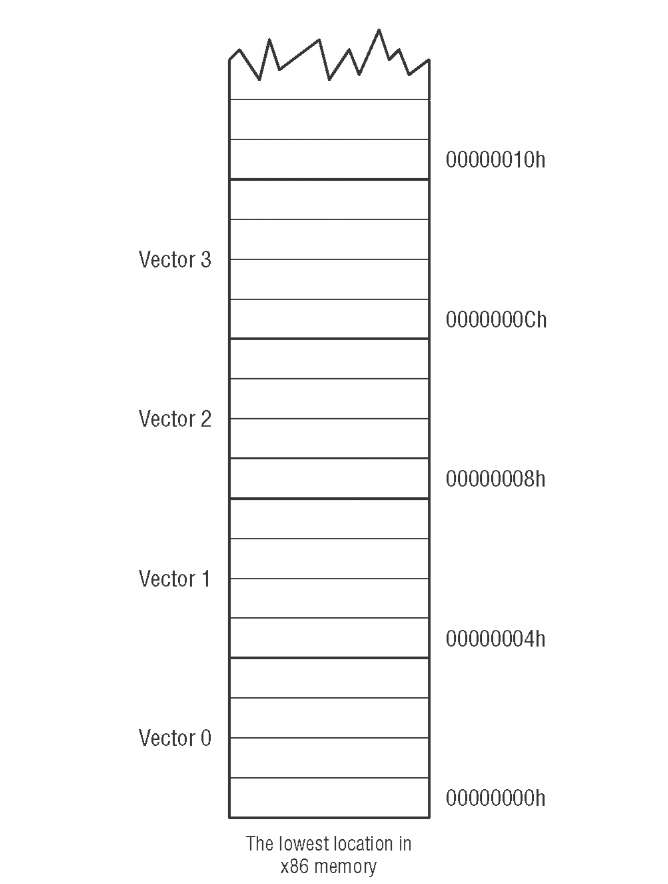
At the very start of x86 memory, down at segment 0, offset 0, is a special lookup table with 256 entries. Each entry is a complete memory address including segment and offset portions, for a total of 4 bytes per entry. The first 1,024 bytes of memory in any x86 machine are reserved for this table, and no other code or data may be placed there.

Each of the addresses in the table is called an interrupt vector. The table as a whole is called the interrupt vector table.

Alt text

mov ecx,EatMsg mov edx,EatLen int 80H

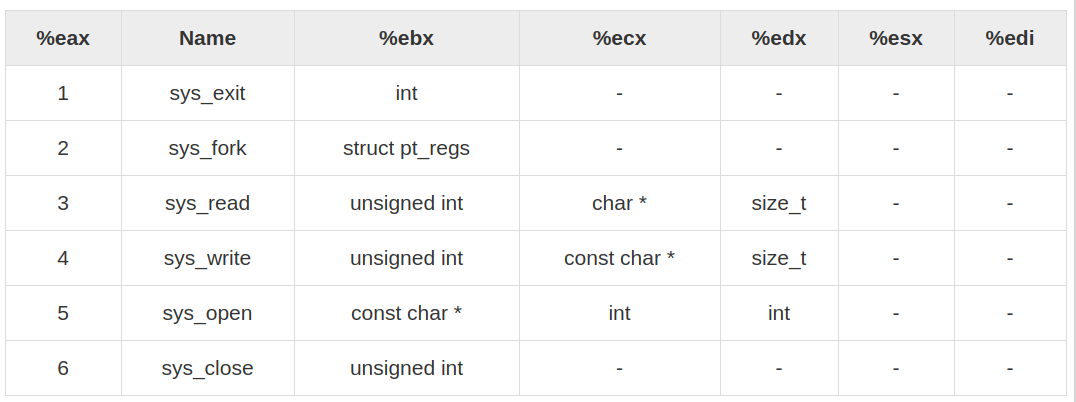
This sequence of instructions requests that Linux display a text string on the console. The first line sets up a vital piece of information: the number of the service that we’re requesting. In this case, it’s to sys_write, service number 4, which writes data to a Linux file. Remember that in Linux, just about everything is a file, and that includes the console. The second line tells Linux which file to write to: standard output. Every file must have a numeric file descriptor, and the first three (0,1, and 2) are standard and never change. The file descriptor for standard output is 1. The third line places the address of the string to be displayed in ECX. That’s how Linux knows what it is that you want to display. The dispatcher expects the address to be in ECX, but the address is simply where the string begins. Linux also needs to know the string’s length, and we place that value in register EDX.

mov eax,1 Specify Exit syscall mov ebx,0 Return a code of zero int 80H Make syscall the to terminate the program

Exiting this way is not just a nicety. Every program you write must exit by making a call to s y s _ e x i t through the kernel services dispatcher. If a program just ‘‘runs off the edge’’ it will in fact end, but Linux will hand up a segmentation fault and you’ll be none the wiser as to what happened.

Software Interrupts versus Hardware Interrupts

hardware interrupts are numbered, and for each interrupt number there is a slot reserved in the interrupt vector table. In this slot is the address of an interrupt service routine (ISR) that performs some action relevant to the device that tapped the CPU on the shoulder

The only real difference between hardware and software interrupts lies in the event that triggers the trip through the interrupt vector table. With a software interrupt, the triggering event is part of the software—that is, an INT instruction. With a hardware interrupt, the triggering event is an electrical signal applied to the CPU chip itself without any INT instruction taking a hand in the process. The CPU itself pushes the return address onto the stack when it recognizes the electrical pulse that triggers the interrupt; however, when the ISR is done, an IRET instruction sends execution home, just as it does for a software interrupt.

Write:	mov eax,4 		;Specify sys_write call
		mov ebx,1 		;Specify File Description 1 standad output
		mov ecx,Buff	;Pass address of the charecter to write
		mov edx,1		;Pass number of chars to write
		int 80H 		;Call sys_write...

EOF.

When you count bits, start with the bit on the right, and number them from 0.

SHL SHifts its operand Left, whereas SHR SHifts its operand Right.

0B76FH is as follows: 1011011101101111 SHL AX,1

0110111011011110

A 0 has been inserted at the right-hand end of the number, and the whole shebang has been bumped toward the left by one digit. The last bit shifted out of the left end of the binary number is bumped into a temporary bucket for bits called the Carry flag, generally abbreviated as CF.

ROL shifts all bits left and moves bit 7 to bit 0. What was 10110010 is now 01100101

nybble??

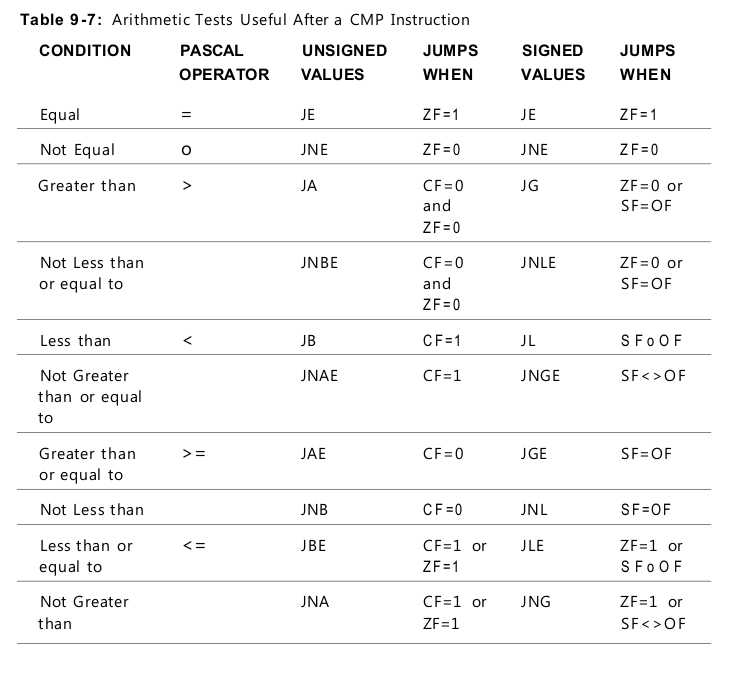
“Greater Than” Versus “Above”

To tell the signed jumps apart from the unsigned jumps, the mnemonics use two different expressions for the relationship between two values: • Signed values are thought of as being greater than or less than. For example, to test whether one signed operand is greater than another, you would use the JG (Jump if Greater) mnemonic after a CMP instruction. • Unsigned values are thought of as being above or below. For example, to tell whether one unsigned operand is greater than (above) another, you would use the JA (Jump if Above) mnemonic after a CMP instruction.

Alt text

The three basic modes of addressing are −

Register Addressing

In this addressing mode, a register contains the operand. Depending upon the instruction, the register may be the first operand, the second operand or both.

For example,

MOV DX, TAX_RATE   ; Register in first operand
MOV COUNT, CX	   ; Register in second operand
MOV EAX, EBX	   ; Both the operands are in registers

Immediate Addressing

An immediate operand has a constant value or an expression. When an instruction with two operands uses immediate addressing, the first operand may be a register or memory location, and the second operand is an immediate constant. The first operand defines the length of the data.

For example,

BYTE_VALUE  DB  150    ; A byte value is defined
WORD_VALUE  DW  300    ; A word value is defined
ADD  BYTE_VALUE, 65    ; An immediate operand 65 is added
MOV  AX, 45H           ; Immediate constant 45H is transferred to AX

BYTE_TABLE DB  14, 15, 22, 45      ; Tables of bytes
WORD_TABLE DW  134, 345, 564, 123  ; Tables of words

The following operations access data from the tables in the memory into registers −

MOV CL, BYTE_TABLE[2]	; Gets the 3rd element of the BYTE_TABLE
MOV CL, BYTE_TABLE + 2	; Gets the 3rd element of the BYTE_TABLE
MOV CX, WORD_TABLE[3]	; Gets the 4th element of the WORD_TABLE
MOV CX, WORD_TABLE + 3	; Gets the 4th element of the WORD_TABLE

Indirect Memory Addressing

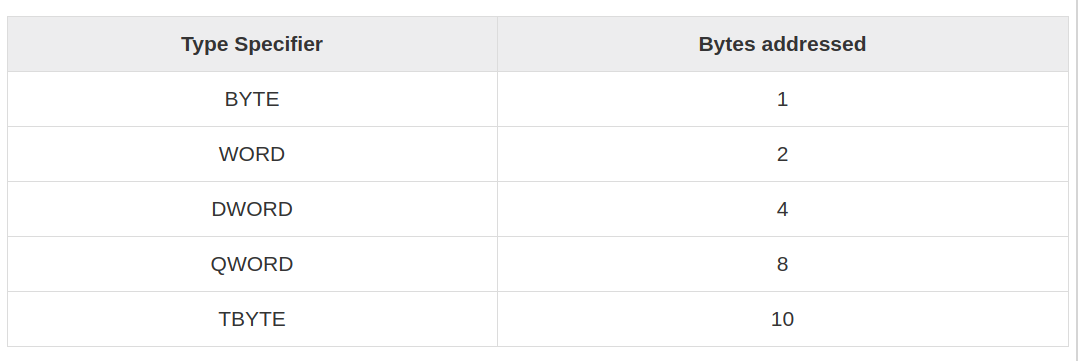
MY_TABLE TIMES 10 DW 0  ; Allocates 10 words (2 bytes) each initialized to 0
MOV EBX, [MY_TABLE]     ; Effective Address of MY_TABLE in EBX
MOV [EBX], 110          ; MY_TABLE[0] = 110
ADD EBX, 2              ; EBX = EBX +2
MOV [EBX], 123          ; MY_TABLE[1] = 123

Alt text

choice		DB	'y'
number		DW	12345
neg_number	DW	-12345
big_number	DQ	123456789
real_number1	DD	1.234
real_number2	DQ	123.456

Each byte of character is stored as its ASCII value in hexadecimal. Each decimal value is automatically converted to its 16-bit binary equivalent and stored as a hexadecimal number. Processor uses the little-endian byte ordering. Negative numbers are converted to its 2’s complement representation. Short and long floating-point numbers are represented using 32 or 64 bits, respectively.

Multiple Initializations The TIMES directive allows multiple initializations to the same value. For example, an array named marks of size 9 can be defined and initialized to zero using the following statement −

marks  TIMES  9  DW  0

Immediate addressing mode

mov A,#23H ; #23H real value

accumilator ??

Direct addressing

mov A,23H ; 23 addess value moves to A

mov 23H,33H ; 33 addess value moves to adress 23

mov 26H,#33H ; 33 value moves to address 26

Register Addessing

you can assign those variables with binary or hexadecimal values. Binary values would need to be appended by the letter ‘b’ at the end of the number. Likewise, hexadecimals with ‘h’ at the end. If the hexadecimal numbers start with letters (i.e. A, B, C, D, E, or F), you need to add a zero in front of that number and add an ‘h’ after that number.

bits  db 101001b
var2  dw 4567h
var3  dw 0BABEh

Similarly, you can load the variables to a register or store them back. You can even transfer values between registers.

mov bx, [our_var]
mov cx, bx
mov [our_var], cx

Note the square brackets when you deal with variables. these square brackets are good to distinguish the variable from its address

There are caveats in using mov command. You CANNOT use mov [var1], [var2]. In other words, mov command cannot transfer values between two variables directly

So, how can we get around with this? Use the register.

Suppose both var1 and var2 are word variables. We can use any word registers (AX, BX, CX, DX, and so on) to do the transfer. Suppose we use AX. Thus, mov [var1], [var2] must be transformed into:

mov ax, [var2] mov [var1],ax

The assembler actually treat variables as a label that has an address in the memory (RAM in most cases) associated to it.

mov will read and write 2 bytes instead of 1. Likewise, using byte register to move a word variable will only transfer one byte instead of two.

 var2 db 2
   var3 dw 305h

start:
   mov ax, [var1]  ; ax now equals to 0201h (i.e. 2*256+1)
   mov ax, [var3]  ; ax now equals to 0305h
   mov ax, [var2]  ; ax now equals to 0502h
   mov al, [var3]  ; al now equals to 05h

MOV EAX,myvar2

The EAX register is now a pointer to myvar2. It does not contain the contents of myvar2 (which may not even be a double word), but it contains the address of myvar2.

Variables as Pointers

Once we have moved an address into a 32 bit register, we are then free to move it into a double word variable for storage.

For example, suppose that EAX has been loaded with the address of some memory location storing a byte of data and suppose that we have a double word variable mypoint, say, that we want to store this address in. We simply write

MOV [mypoint],EAX

Now here comes the tricky part. Let’s suppose we want to load the contents of the memory location now pointed to by mypoint, into the CH register. Firstly we have to retrieve the address from storage:

MOV EBX,[mypoint]

Now EBX points to the location in question. Now to retrieve the byte of data at that location, we write

MOV CH,[EBX]

Here the square brackets do not denote the contents of EBX itself (for which we would just write EBX), but rather, they denote the contents of the location pointed to by EBX.

Although this usage of the square brackets may seem different to the earlier usage, it is in reality the same thing, since the thing inside the brackets is basically a pointer in both cases.

EAX used to be called the accumulator since it was used by a number of arithmetic operations, and ECX was known as the counter since it was used to hold a loop index. Whereas most of the registers have lost their special purposes in the modern instruction set, by convention, two are reserved for special purposes — the stack pointer (ESP) and the base pointer (EBP).

.DATA			
var	DB 64  		; Declare a byte, referred to as location var, containing the value 64.
var2	DB ?	; Declare an uninitialized byte, referred to as location var2.
DB 10			; Declare a byte with no label, containing the value 10. Its location is var2 + 1.
X	DW ?		; Declare a 2-byte uninitialized value, referred to as location X.
Y	DD 30000    ; Declare a 4-byte value, referred to as location Y, initialized to 30000.

C pointer

#include <stdio.h>	
int main () {

   int  var = 20;   /* actual variable declaration */
   int  *ip;        /* pointer variable declaration */

   ip = &var;  /* store address of var in pointer variable*/

   printf("Address of var variable: %x\n", &var  );

   /* address stored in pointer variable */
   printf("Address stored in ip variable: %x\n", ip );

   /* access the value using the pointer */
   printf("Value of *ip variable: %d\n", *ip );

   return 0;
}

assebmly        | c language
----------------|------------
mov eax,ebx 	| eax  = ebx
mov eax,[ebx] 	| eax  = *ebx
mov [eax],ebx 	| *eax = ebx
mov eax,[myvar] | eax  = myvar
mov eax,myvar 	| eax  = &myvar

assembly number differnces decimal or hex or ansi??

Numerical data is generally represented in binary system. Arithmetic instructions operate on binary data. When numbers are displayed on screen or entered from keyboard, they are in ASCII form.

proc_name: procedure body … ret The procedure is called from another function by using the CALL instruction. The CALL instruction should have the name of the called procedure as an argument as shown below −

CALL proc_name

Alt text

The C, C++, C#, Java, and other C-derivative programming languages use the prefix “0x” to denote a hexadecimal value. Therefore, you’d use the character sequence “0xdead” for the hexadecimal value DEAD16

So for hexadecimal values that don’t already begin with a numeric digit, you would add “0” to the beginning of the value (adding a zero to the beginning of any numeric representation does not alter the value of that representation). For example, use “0deadh” to unambiguously represent the hexadecimal value DEAD

101.01 The conversion to decimal yields: 1 × 2^2 + 1 × 2^0 + 1 × 2^-2 = 4 + 1 + 0.25 = 5.25

Older Newer

Teymur Valiyev Weblog

Algorithms

Permutation

Permutation with Identical items

Combinations

Sum

Example 1

Solution

Example 2

Solution

Strategy

Brute Force

Backtracking

Heuristics

Greedy Algorithms

Divide and Conquer (D&C)

Example:

Dynamic Programming

Branch and Bound

Algorithm Complexity

Algorithm falls under three types

Computational Complexity

Common Asymptotic Notations

Constant Time

Linear Time

Quadtic Time

Divide and Conquer (D&C)

Divide-and-conquer

Average case vs. worst case

Categories of algorithms

Algorithm Complexity

Algorithm falls under three types

Common Asymptotic Notations

Greedy Algorithms

The Knapsack problem

The set-covering problem

Approximation algorithms

Dynamic Programming

The Feynman algorithm

Longest common subsequence

Longest common substring

Levenshtein distance

k-nearest neighbors

Pythagorean formula

Cosine similarity

Dynamic Programming

Sorting and Searching Algorithms

Sorting algorithms

Selection sort

Selection sort

Bubble sort

Insertion Sort

Merge sort

Quicksort sort

Binary search

Example

Some common Big O run times

Traveling salesperson problem.

Tree

Binary search tree

Inverted indexes

The Fourier transform

Parallel algorithms

MapReduce

Distributed algorithm

Interpolation Search

Hash Table

Collisions

Load factor

Arithmetic Sets

Membership

Equality

Unions

Intersections

Complements

Universal set and absolute complement

Subsets

Proper Subsets (strict subsets)

Posibile Subset

References